About me and why I created this physics website.
The Physics Of Pole Vaulting
Have you ever watched pole vaulting in the Olympics? As a kid, I loved the track and field events, and pole vaulting was a fun event to watch. I remember the excitement I felt as I watched the athletes attempt to vault over the bar. Would they clear it or would they knock it down? Little did I understand then the major role that physics plays in making a successful vault.
Pole vaulting is an athletics event in which a person uses a long flexible pole as an aid to jump over a bar. Pole vaulting has been an event at the Olympic games since 1896.
The basic physics of pole vaulting is simple to explain. The pole vaulter must run as fast as he or she can, and then convert the corresponding kinetic energy of the run into maximum height using proper vaulting technique. The faster the vaulter runs, the greater their kinetic energy, and the higher they can vault.
Source: http://en.wikipedia.org/wiki/Pole_vault. Author: http://commons.wikimedia.org/wiki/User:Jastrow
To express the basic physics in mathematical terms, we must equate the kinetic energy of the vaulter to the gravitational potential energy corresponding to the point of maximum height.
Therefore,
(1/2)MV2 = Mg(Δh)
Where:
M is the mass of the pole vaulter
V is the velocity of the pole vaulter just before the vault
g is the gravitational constant, equal to 9.8 m/s2
Δh is the change in height of the pole vaulter's center of mass
Note that at the point of maximum height we can assume that the kinetic energy is zero. And it is also assumed that all the kinetic energy of the vaulter is converted into gravitational potential energy. This is the ideal situation. But in reality, not all the kinetic energy is converted into gravitational potential energy. There are unavoidable energy losses, as there are in all real-life systems.
From the above equation,
Δh = (1/2)V2/g (the mass M cancels out)
For example, let's say a male pole vaulter with center of mass approximately 1.0 m off the ground, runs at 10 m/s. According to the above equation, this yields Δh = 5.10 m. Since his center of mass is 1.0 m off the ground, this means that his vault height (off the ground) is 6.10 m.
The above equation agrees very well with real life. The theoretical height calculated by this equation closely matches the actual height reached by athletes, based on their running speed V just before they start the vault.
Top-level pole vaulters can in fact run at about 10 m/s, which is excellent sprinting speed given that they must also carry the vaulting pole.
Contrary to what many believe, pole vaulters do not use their strength to lift themselves over the bar. Instead, they primarily use the pole as an intermediate tool to help them convert their kinetic energy into gravitational potential energy (height). Good sprint speed combined with good gymnastic ability are what is needed to effectively utilize the pole.
Naturally, the pole must be as light as possible as this enables the vaulter to run as fast as possible before take-off.
The pole must also be very elastic in bending as this will allow the vaulter to efficiently transfer his kinetic energy to the pole in the form of elastic potential energy, and this pole energy is then transformed into gravitational potential energy as the pole straightens itself out and the vaulter reaches the top of the vault.
During the pole plant, some energy is unavoidably lost as the end of the pole collides with the take-off box. But this energy loss is minimised by using proper technique at take-off.
To maximize vault height, vaulters bend their body around the bar (as shown in the figure below). In doing so, their center of mass (the red dot) can actually pass underneath the bar, while enabling their body to pass over the bar (the black dot). This means that the bar can actually be placed higher than the maximum height reached by the center of mass of the vaulter.
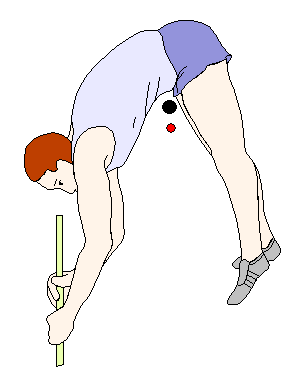
However, at the top of the vault, some kinetic energy must actually remain so that the vaulter does not fall down into the bar. This means that the vaulter must possess some horizontal velocity in order to laterally cross over the bar. But even if the horizontal velocity is 1.0 m/s this will only reduce the height predicted by the above equation by about 5.0 cm, which is very little difference.
Air resistance also plays a role in how high a vaulter can vault. In areas of higher altitude, the air is less dense which reduces air resistance when running. This in turn means that the vaulter can reach a higher speed before the vault, which results in a higher vault. To give you an idea, if a vaulter running at 10 m/s at sea level can run 2% faster at high altitude, then he can vault about 21 cm higher at high altitude.
That wraps it up. Hopefully I was able to give you a good sense of the physics behind pole vaulting.
Have a look at the world outdoor record vault of 6.14 m, set by Sergey Bubka of the Ukraine, in 1994.
Return to The Physics Of Sports page
Return to Real World Physics Problems home page