About me and why I created this physics website.
The Physics Of Luge
The basic principle behind the physics of luge is to navigate the track as fast as possible. This is done by maximizing starting speed, and minimizing the forces which act to slow the luger down after the start.
The picture below shows a luger at the start of the race.
Source: http://www.flickr.com/photos/jonwick/4363939510
The luger maximizes his starting speed by rocking himself back and forth using the side handles shown, to build up speed, before launching himself forward. After release, he further increases his speed by pushing off the ice with his hands. Luge gloves are spiked in order to maximize friction with the ice during this stage of the start.
Once the luger has gained as much speed as he can off the start, he then lies back on the sled. At this point gravity takes over.
Since gravity is the only force that increases the speed of the luger once he gets going (after the start), it follows that the fastest time on the track is largely determined by the luger who minimizes those factors that slow him down. These factors are: air resistance, sliding friction with the ice, and inefficient navigation along the straight and turn portions of the track. When it comes to optimizing speed, these are the most important considerations in the physics of luge, and much effort goes into addressing them.
Air resistance is caused by the force of air pushing against the luger and sled, in a direction opposite the luger's motion. This is commonly referred to as drag force and is expressed mathematically by the following equation:
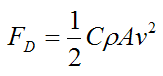
Where:
FD is the drag force acting on the luger and sled
C is the drag coefficient, which can vary along with the speed of the luger. But typical values range from 0.4 to 1.0
ρ is the density of the air
A is the projected frontal area of the luger and sled, perpendicular to the flow direction (that is, perpendicular to his velocity v)
v is the velocity of the luger relative to the air
Drag force is an important aerodynamic consideration in the physics of luge, so minimizing it is very important. As evident in the above equation, the luger can minimize the drag force by minimizing the projected frontal area A. He does this by keeping his body as flat as possible on the sled, while also keeping his feet pointed forward as much as possible, and his head as low as possible. His head must be held just high enough for him to see the track ahead of him.
The equipment used is also an important aerodynamic consideration in the physics of luge. The sled must be sturdy and aerodynamic. The race suit and boots must be smooth and skin-tight to reduce aerodynamic drag. The helmet must be smooth and aerodynamic with the visor extending below the luger's chin. This eliminates air pockets which can increase drag.
The mass of the luger can also help counteract the drag force FD. A greater mass means a greater force of gravity acting on the luger, which means that the relative magnitude of FD becomes smaller. As a result, a heavier luger reaches a greater velocity v than a lighter luger (with all else being equal).
The sliding friction of the sled with the ice is minimized by polishing the steel blades of the sled so that they are as smooth as possible. The blades are the only part of the sled in contact with the ice (the blades are on the bottom edge of the runners).
The blades of the sled are sharpened, which allows them to "bite" into the ice. This helps the sled maintain a smooth straight arc along the turns, with little up and down movement.
The luger steers by pressing against one of the two runners with his calf, or by making small movements with his shoulders to shift his weight. Pressing against the runners changes the angle the blades make with the ice. It's similar to how a bike turns by changing the angle of the front wheel. Given the high speeds lugers reach on the track, only slight changes in blade angle are needed to cause a significant amount of steering.
The amount of steering a luger does must be kept to a minimum since the act of steering increases the level of friction between the blades and ice.
The final factor a luger must deal with to minimize race time is navigate the track as efficiently as possible. He does this by minimizing the distance traveled along the track, while also minimizing the amount of steering done (since this reduces friction with the track).
This means that on the straight sections of the track, the luger must go as straight as possible (without rubbing against the sides of the track). However, on the turning sections of the track, the luger must ride up the side of the banked curves (of the turns) just the right amount, so that he travels a theoretical perfect line along the turn. This theoretical perfect line exists because the bank angle of the turn increases the farther up the side you go. This theoretical perfect line is such that the combination of distance traveled, and the amount of steering required (along the turn), results in a minimum travel time (along the turn). For a travel path above this theoretical perfect line, the radius of the travel path along the turn is excessive, and results in excessive distance traveled (along the turn). This increases the travel time. For a travel path below this theoretical line, extra steering effort is required. This creates extra friction with the ice, which slows down the sled excessively. The net effect is an increase in travel time, even though the distance traveled is less.
As an analogy, consider Nascar racing. The driver steers less when going around banked turns than he would if the turns were flat (no bank angle). This analogy helps explain why a luger has to steer more on the lower part of the turns than on the higher part of the turns.
The two pictures below show a luger on the straight part of the track and on the turning part of the track.
Source: http://www.flickr.com/photos/jonwick/4363230159
Source: http://www.flickr.com/photos/kpedraja/4364849234
In the picture above, the blue arrow shows the theoretical perfect line that the luger must travel to get the fastest time around the turn. This perfect line is largely determined by experience. But it would also be an interesting area of research for anyone studying luge physics.
In the next section we will look at the centripetal acceleration a luger experiences when going around a turn.
Centripetal Acceleration
The centripetal acceleration (ac) a luger experiences when going around a turn is given by
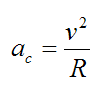
where v is the velocity of the luger and R is the radius of the turn that he makes.
The speed reached by lugers on a track can be as high as 140 km/h. This can translate into a centripetal acceleration of 5g (which is 5 times the force of gravity – where the acceleration due to gravity is 9.8 m/s2). For a speed of 140 km/h, 5g corresponds to a turn radius of 30.9 meters.
Banked Turns
The banked curves of the turns are necessary because they help the luger stay on the track as he goes around the turns. A banked turn creates a normal force (perpendicular to the track) that has a component acting in the same direction as the centripetal acceleration (which acts towards the center of the turn). This normal force component (the centripetal force) is what helps the luger go around the turn, without slipping. If the luger were to go around a flat horizontal turn (with no bank angle), the normal force would have no component in the direction of the centripetal acceleration. This means that the luger would have to rely solely on the horizontal force of the ice pushing against the side of the runner blades (which are pressed into the ice), in order to go around the turn. Given the high centripetal force created during the turns, this would be very difficult to do, thus necessitating the need for banked turns.
Closing Remarks
Clearly, minimizing the time it takes to travel the track depends on optimal equipment, along with the technical skill and athletic prowess of the luger. This is a sport where thousandths of a second count, which can make the difference between winning and losing. And like all modern high-performance sports, it requires lots of training and sound scientific knowledge in order to excel at it.
Return to The Physics Of Sports page
Return to Real World Physics Problems home page