About me and why I created this physics website.
Pendulum Physics
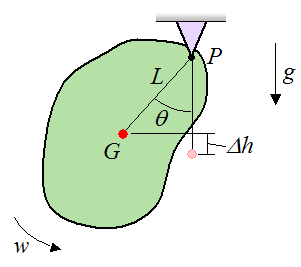
To analyze the physics of a pendulum, consider the figure below which shows an arbitrary rigid body swinging back and forth in a plane, about a pivot P. This swinging is due to the force of gravity.
Where:
w is the angular velocity of the rigid body at the instant shown, in radians/s
P is the (fixed) pivot location
G is the location of the center of mass of the rigid body
L is the distance from point P to point G
θ is the angle between the vertical and the line joining points P and G, at the instant shown
Δh is the difference in height of point G, between the lowest point of the swing (chosen as the datum), and at the instant shown
g is the acceleration due to gravity, which is 9.8 m/s2 on earth
We wish to find the equation of motion for this rigid body.
In analyzing pendulum physics a common simplification is to assume no friction at the pivot P. Using this assumption we can apply the principal of conservation of energy for the pendulum. This principal states that the sum of the gravitational potential and kinetic energy of the pendulum remains constant over time. In other words,
Where:
W is the gravitational potential energy of the pendulum at an instant
KE is the kinetic energy of the pendulum at an instant
C is a constant
The gravitational potential energy of the pendulum is:
where m is the mass of the rigid body, and
Therefore,
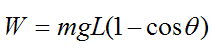
The kinetic energy of the pendulum is:
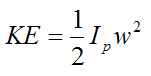
where Ip is the moment of inertia of the pendulum about an axis passing through point P (this axis is perpendicular to the plane of motion, so that it points out of the page)
Furthermore,
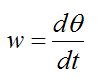
Applying the above equation for the conservation of energy for the pendulum we have,
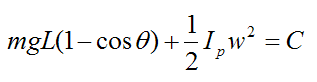
Next, differentiate this energy equation with respect to time. This is a convenient way to obtain the equation of motion for the pendulum. We get,
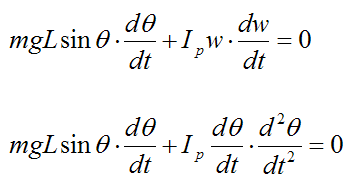
This becomes:
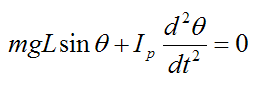
A common simplification when analyzing pendulum physics is to assume that θ is small, so that
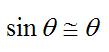
Therefore,
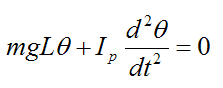
This is a second order differential equation. It has the general solution:
where t is time, and A and φ are constants, which can be calculated based on the (prescribed) initial conditions of the pendulum at time t = 0.
In the above equation, the constant B is:
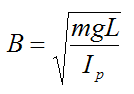
A specific case is to assume that we have a simple pendulum, instead of a rigid body, as shown below.
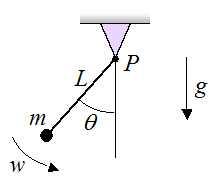
In a simple pendulum the mass m is assumed to be concentrated in one point (point mass), and is attached to the end of a rigid rod of length L and negligible mass.
For a simple pendulum the moment of inertia about point P is:
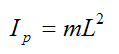
and
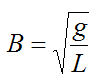
The period of oscillation T for the general pendulum is:
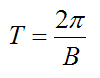
This is the time it takes to complete one full cycle, or “swing”.
The frequency f in hertz (Hz) is defined as the number of cycles per second. For a general pendulum the frequency is:
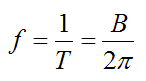
To illustrate the motion of a pendulum, let's look at a specific case, where the amplitude A = 2, the constant B = 1, and φ = 0. The figure below illustrates the sinusoidal motion.
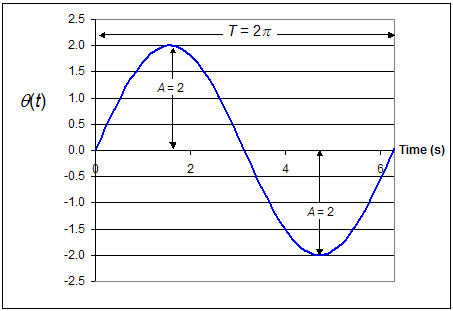
The motion shown in this graph is sometimes called simple harmonic motion.
Return to Miscellaneous Physics page
Return to Real World Physics Problems home page
