About me and why I created this physics website.

Motion Along A Circular Path

A body is rotating as shown below.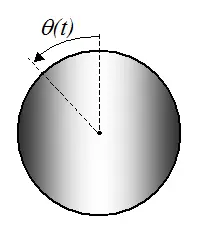




Define the following variables:

θ(t) is the angular rotation as a function of time

Δθ is the change in angle (angular displacement)

w is the angular velocity

α is the angular acceleration

t is time


Now,





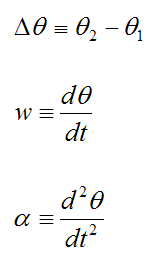
If we assume constant angular acceleration, we have the following formulas. Note that the subscripts 1 and 2 denote "initial" and "final".





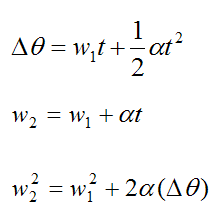
These formulas apply to every particle in a rigid body that is experiencing rotation, such as the disk shown in the first figure. In other words, all the particles experience the same angular displacement, angular velocity, and angular acceleration regardless of their position relative to the center of rotation.



Return to Useful Physics Formulas page


Return to Real World Physics Problems home page