About me and why I created this physics website.
Momentum And Collisions
A particle of mass m is moving at velocity v.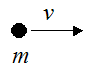
The linear momentum is defined as:
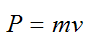
Impulse is defined as an average force F acting for a time Δt (this time is typically short). Mathematically, impulse is FΔt.
If an impulse acts on a particle of mass m, its momentum will change by an amount ΔP. We can express this as:
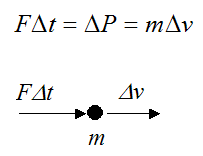
where Δv is the change in velocity of the particle.
Conservation Of Linear Momentum
When two objects collide, momentum is conserved. The figure below shows a collision between two objects (before and after).
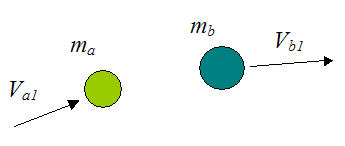
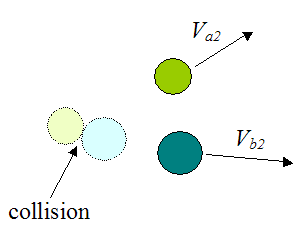
Where:
Va1 is the initial velocity of object a, before collision
ma is the mass of object a
Vb1 is the initial velocity of object b, before collision
mb is the mass of object b
Va2 is the final velocity of object a, after collision
Vb2 is the final velocity of object b, after collision
The vector equation for conservation of linear momentum can be expressed as:
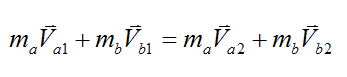
For all three directions in x, y, z this becomes:
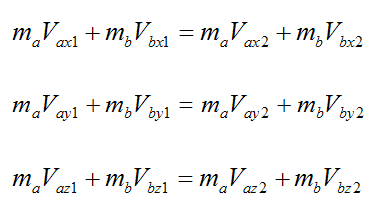
For an elastic collision, kinetic energy is conserved. Thus,
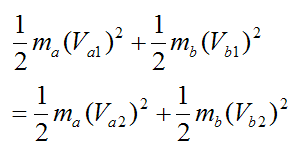
For elastic collisions in one-dimension (head-on collision):
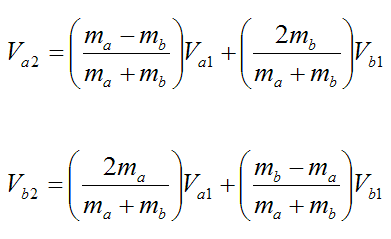
Conservation Of Angular Momentum
The angular momentum L for a body rotating about a fixed axis is defined as:
Where:
I is the rotational inertia of the body about the axis of rotation
w is the angular velocity of the body
If no net external torque acts on the body, L = constant.
Thus,
where the subscripts 1 and 2 denote "initial" and "final".
For example, a figure skater pulling his arms in during rotation will spin faster as a result. This is because there is no net external torque acting on his body. So as he pulls in his arms he is decreasing his I value, which results in w increasing (since his angular momentum L is constant).
Return to Useful Physics Formulas page
Return to Real World Physics Problems home page