About me and why I created this physics website.
How Hot Is The Sun?
At some point you may have wondered, how hot is the Sun? If so, you're in good company, since it's a very common physics-related question. The answer really depends on what part of the Sun you're referring to. Different regions of the Sun have different temperatures. For example, the core of the Sun has a temperature of about 15 million degrees Celsius, and the outermost layer of the Sun's atmosphere (called the corona) has a temperature of about 1-2 million degrees Celsius. The temperature of the surface of the Sun is directly related to how much solar energy the Sun produces, which is then radiated out from the surface into space. The planet Earth receives only an extremely tiny percentage of the total solar energy produced by the Sun. The picture below shows a view of the Sun as seen from here on Earth. If you're simply asking what the surface temperature of the Sun is, you're referring to the part of the Sun that we most readily see, which is what is shown in the picture.
Source: https://commons.wikimedia.org/wiki/File:Sun_(Earth_POV).jpg. Author: DracoLumina17
Did you know that you can easily calculate the surface temperature of the Sun? Trust me, this is much more interesting than just giving you the answer! If you know the radius of the Sun, the distance of the Earth from the Sun, and the solar power density at the location of the Earth, you can calculate it. The figure below illustrates this.
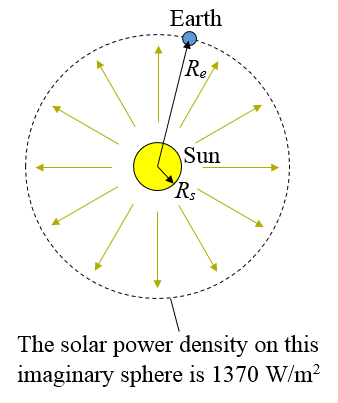
By energy conservation, the power (energy/second) emitted at the Sun's surface is equal to the power received at the imaginary sphere surface. The Sun's energy is emitted in all directions uniformly. This means that at an arbitrary distance from the center of the Sun, the power density is uniform over an imaginary sphere surface, whose radius is equal to this distance. From measurements taken in space, such as from a satellite, we know that the solar power density from the Sun is 1370 W/m2, outside of Earth's atmosphere. Note that it is important to measure the solar power density outside the Earth's atmosphere, and not on Earth's surface, since Earth's atmosphere absorbs some of the solar energy. As a result, measuring the solar power density on Earth's surface is not an accurate measure of the solar power density received at the imaginary sphere surface.
Next, let the radius of the Sun be Rs, and let the distance of the Earth from the Sun's center be Re (this is the radius of the imaginary sphere).
All of the energy emitted by the Sun is in the form of electromagnetic radiation. The power density emitted at the Sun's surface is approximately given by the following Stefan-Boltzmann equation, which assumes that the Sun emits electromagnetic radiation as a black body: P = (5.67 × 10-8)T4, where P is the power density emitted in units of W/m2, and T is the surface temperature of the Sun in units of Kelvin.
By energy conservation, P×(surface area of Sun with radius Rs) = 1370×(surface area of imaginary sphere with radius Re).
Next, substitute the formulas for the surface area of a sphere, having radius Rs and Re. The result is,
P×(4πRs2) = 1370×(4πRe2). Use Rs = 6.96 × 108 m, and Re = 1.5 × 1011 m, which is an average value since the distance between the Earth and Sun is not fixed and it varies a bit over time.
Solve for T. The result is T = 5800 Kelvin, which is about 5500 degrees Celsius. This is the surface temperature of the Sun.
References
https://www.acs.org/content/acs/en/climatescience/energybalance/energyfromsun.html
https://www.ess.uci.edu/~yu/class/ess200a/lecture.2.global.pdf
Return to Miscellaneous Physics page
Return to Real World Physics Problems home page