How Airplanes Fly
The purpose of this page is to provide an overview of how airplanes fly. The study of flight is actually a vast subject in the field of aerodynamics which reaches far beyond what is discussed here. The study of flight combines wind tunnel testing, similarity scaling principles, analytical modeling, computational fluid dynamics (CFD), and empirical test data found in charts and tables. Nevertheless, this page will at least help you to conceptualize the basic principles of how airplanes fly, and will be a useful resource for the beginner.How Airplanes Fly – Aerodynamic Forces
Airplanes are constructed such that the airflow pattern around them generates lift, thereby enabling them to fly. The airflow in turn is produced by the forward motion of the plane relative to the air. This forward motion is produced by engine thrust, delivered by way of propeller engines or air-breathing engines (turbines). Airplane engines produce thrust by accelerating the airflow in the rearward direction. This backwards acceleration of the airflow exerts a "push" force on the airplane in the opposite direction, by Newton's third law, causing the airplane to move forward.
All the forces (and moments) acting on an airplane are a result of pressure forces (normal to the airplane surfaces) and shear forces (along the airplane surfaces), both created by the airflow pattern over the airplane body. The moments (torques) are a result of the forces and, in addition to forces, are part of rigid body motion analysis. Airplanes can generally be treated as rigid bodies when analyzing the dynamics of their motion.
The lift force "holding" a plane up is generated by airflow over the wings. This airflow is only possible if the plane moves relative to the air, hence lift is only possible if the plane moves relative to the air. And the relative air speed must be large enough for sufficient lift to be generated.
In the next section we will discuss airfoils.
Airfoils
In aerodynamics, airplane wings are called airfoils. They have a cambered shape which enables them to produce lift, even for angles of attack (α) equal to zero. The figure below shows a cross-sectional view of an airfoil, with nomenclature shown.
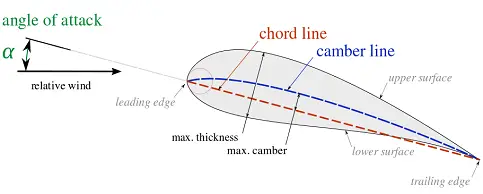
Source: http://en.wikipedia.org/wiki/Airfoil. Author: http://commons.wikimedia.org/wiki/User:Ariadacapo
The orientation of the airfoil relative to the airplane body is shown below. The angle of incidence is defined as the angle between the chord line and the longitudinal axis of the plane. For general aviation designs, an angle of incidence commonly used is about 6 degrees.
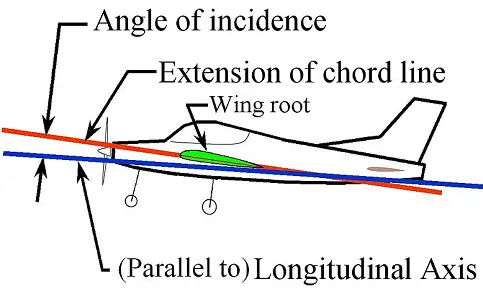
Source: http://en.wikipedia.org/wiki/Angle_of_incidence
The figure below shows airflow over an airfoil.
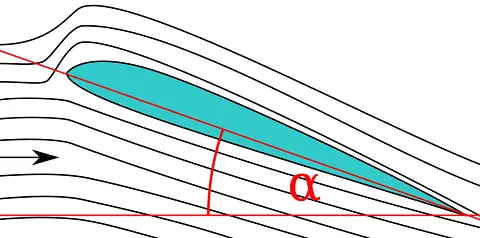
Source: http://en.wikipedia.org/wiki/Angle_of_attack. Author: http://en.wikipedia.org/wiki/User:Theresa_knott
The presence of air friction (viscosity) is what allows an airfoil to generate lift. The reasoning behind this is complicated and involves rather complex mathematics. But basically, the air flow pattern around an airfoil results in the lower half of the airfoil experiencing greater pressure force than the top half of the airfoil. As a result, a lift force is generated. This is perhaps the least understood, and most asked, aspect of how airplanes fly.
In the next section we will discuss in greater detail the forces acting on an airplane during flight.
Forces Acting On An Airplane
The figure below shows the resultant forces acting on an airplane in level flight, moving at constant velocity.
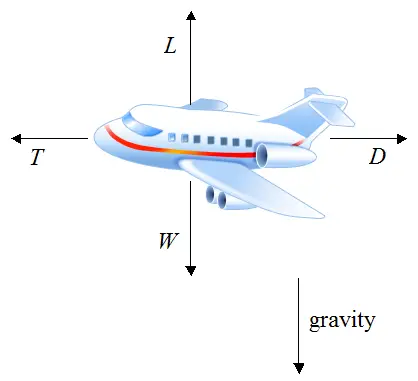
Since the airplane is moving at constant velocity it is experiencing zero acceleration, and the forces must balance. This means that the lift force (L) generated by the airplane wings must equal the airplane weight (W), and the thrust force (T) generated by the airplane engines must equal the drag force (D) caused by air resistance.
An airplane undergoing takeoff, or landing, experiences similar forces acting on it. The figure below shows the typical forces acting on an airplane during takeoff. Note that the lift force (L) is defined as perpendicular to the velocity (V) of the plane relative to the air. The drag force (D) is defined as parallel to the velocity (V). As one would expect, the thrust force (T) is in the same direction as (V). The weight (W) of the plane points straight down in the direction of gravity. Now, W = mg, where m is the mass of the plane and g is the acceleration due to gravity, where g = 9.8 m/s2.
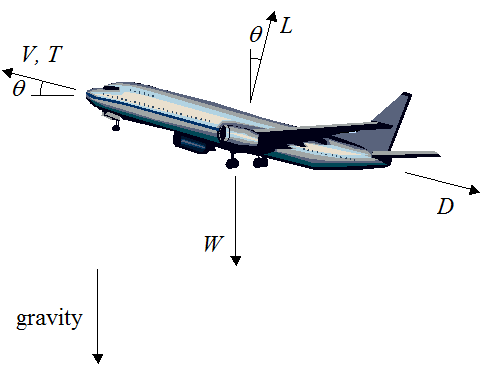
If the plane is moving at constant velocity with respect to ground then all the forces acting on the plane must be balanced. This means that in the vertical direction the sum of the forces is equal to zero, and in the horizontal direction the sum of the forces is equal to zero. Mathematically, in the vertical direction: Lcosθ + Tsinθ − Dsinθ − W = 0. In the horizontal direction: Tcosθ − Dcosθ − Lsinθ = 0. If the plane is experiencing acceleration one can account for this in the force equations, by including acceleration terms in the force equations, using Newton's second law.
In the next section we will discuss how airplanes adjust their attitude and flight path.
Maneuvering And Navigation
Airplanes control their navigation path and attitude (orientation relative to the direction of air flow) by adjusting physical elements on the outside of the airplane, elements which modify the airflow pattern around the plane, causing the plane to adjust its attitude and flight path. These physical elements are called control surfaces and consist of ailerons, elevators, rudders, spoilers, flaps, and slats. Adjusting a plane's flight path always involves either pitching, rolling, or yawing, or a combination of these. The figure below illustrates what these are.

Source: http://en.wikipedia.org/wiki/Flight_dynamics_%28fixed_wing_aircraft%29. Author: http://commons.wikimedia.org/wiki/User:ZeroOne
For example, let's say a plane is to go around a horizontal turn. For a plane to make a turn its body orientation must be tilted (roll) such that the resulting aerodynamic forces enable the plane to go around a turn. Lateral forces enabling a turn are only possible by tilting the airplane such that the lift force (L) has a lateral component needed to balance the centripetal acceleration produced during the turn. The figure below illustrates this.
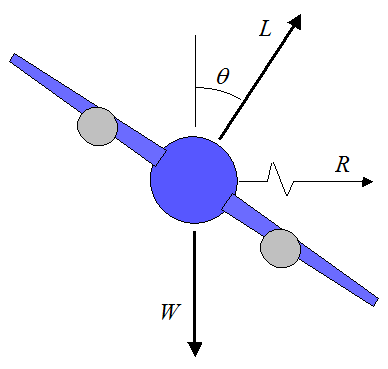
We can analyze this as follows.
By Newton's second law, the force balance for the centripetal acceleration, in the lateral direction, is given by
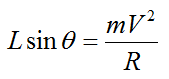
where θ is the bank angle, m is the mass of the plane, V is the velocity of the plane (normal to the page) with respect to ground, and R is the radius of the turn.
The force balance in the vertical direction is given by
Combine the above two equations to give the radius of the turn. We have
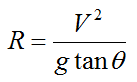
Another example of a situation where flight path needs to be adjusted occurs if there is a wind blowing in a direction different from the direction the pilot want to go, with respect to ground. For example, let's say there is a lateral wind blowing, which results in the plane being "carried" in the direction of the wind. And let's further say that the pilot want to fly straight ahead. To compensate for the wind, the pilot must fly at a certain angle relative to the air such that the plane's flight with respect to ground is in the desired direction. The figure below illustrates this.
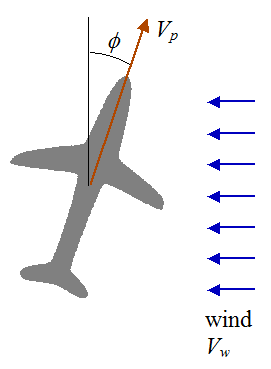
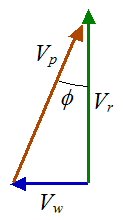
where Φ is the angle with respect to the desired direction of travel, Vw is the wind velocity with respect to ground, Vp is the plane velocity with respect to the air, and Vr is the resultant plane velocity with respect to ground.
Using vector addition we can construct the following vector diagram. The angle Φ and the velocity Vp must be selected such that the resultant velocity vector Vr is in the desired direction.
On a related note, planes will often fly in high altitude jet streams. These are fast flowing air currents. A plane can be "carried" by a jet stream and as a result dramatically reduce flight time if the jet stream is flowing in the intended direction of travel. Of further benefit, high altitude flight also reduces the drag force since air has much lower density at high altitude. To understand this consider the drag force equation: D = (1/2)CρAv2, where C is the drag coefficient, ρ is the density of the air through which the airplane is moving, A is the projected cross-sectional area of the airplane body perpendicular to the flow direction (that is, perpendicular to v), and v is the speed of the airplane relative to the air. As you can see, drag force is proportional to density, and lower drag force results in greater fuel efficiency since less engine thrust is needed to overcome the drag force.
Next we will discuss supersonic flight.
Supersonic Flight
Virtually all commercial aircraft fly at subsonic speeds, which are speeds (relative to the air) less than the speed of sound (which is approximately 340 m/s). As a result, such aircraft have aerodynamic design suitable for these speeds. For example, the airfoil shapes shown previously are designed for subsonic flight.
In supersonic flight, the aircraft speed relative to the air is greater than the speed of sound. This requires a significant difference in aerodynamic design from that of aircraft flying at subsonic speeds. The basic reason for this is that air carries "information" in the form of pressure waves at a certain speed (i.e. the speed of sound), which varies with air temperature, and air density. These pressure waves are due to the physical movement of objects in contact with the air.
An object moving through the air creates disturbances in the air directly in contact with the object. These disturbances (in the form of pressure waves) then travel away from the object, in all directions, through the air, at the speed of sound. For an object moving at less than the speed of sound (relative to the air), the disturbances traveling upstream of the object do so at a speed faster than the object. As a result, the air upstream of the object can "react" quickly enough to accommodate the passage of the object through the air. Hence, the airflow around an object moving at subsonic speeds can smoothly flow around the object.
For an object moving at supersonic speeds, the air upstream of the object cannot react quickly enough to adjust for the presence of the object as it moves through the air. As a result, air "piles up" against the object in a violent and sudden manner. This results in the formation of shock waves, which is heard as a sonic boom. The presence of these shock waves necessitate a different wing design than that used for aircraft flying at subsonic speeds. Typically, supersonic wing designs have a delta shape, which create sufficient lift, while also weakening the shock waves, and as a result this reduces the drag force. The figure below shows a top view of a jet experiencing shock waves during supersonic flight speed. The figure shows what typical shock waves might look like, coming off the front tip and the wing tips. Shock waves are an important part of the physics of how airplanes fly, at supersonic speeds.
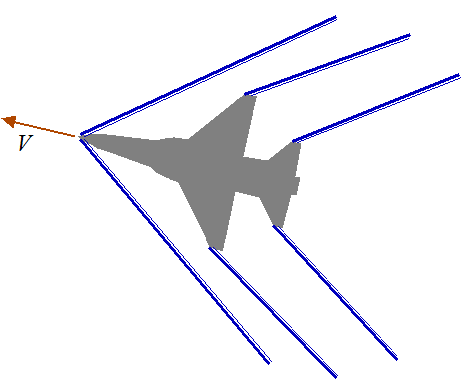
Delta wing designs must also be suitable for subsonic flight since takeoff, landing, and occasional cruising speeds, are subsonic.
Lastly, we will discuss hypersonic flight.
Hypersonic Flight
For aircraft flying at hypersonic speeds, which are usually defined as speeds greater than Mach 5 (5 times the speed of sound), significant problems can arise due to extreme heating of the aircraft body caused by the intense frictional dissipation of air within the boundary layer on the aircraft surface. The space shuttle, during re-entry into the earth's atmosphere, travels at about Mach 25 which is why its design (delta wing shape), attitude, and flight path must be such that surface heating is minimized. Failure to do this will result in the shuttle burning up during re-entry.
During re-entry the space shuttle adjusts its angle of attack (α) so that it becomes a "blunt body" with respect to the air flow. This is shown in the figure below.
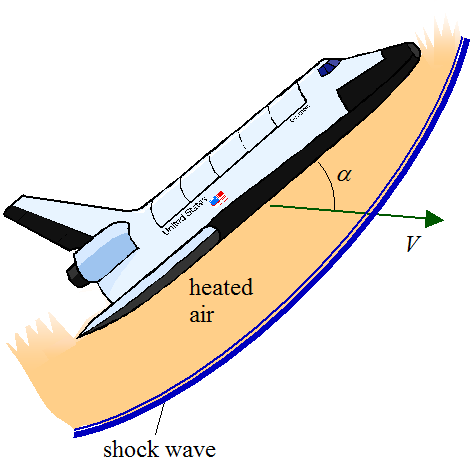
The shuttle enters at a small entry angle, relative to the earth, and with a large angle of attack. The angle of attack is approximately 40 degrees during the re-entry, and this angle is maintained by the shuttle control systems. This large angle of attack minimizes the heating of the shuttle. This is because the resulting strong shock wave near the base of the shuttle, which is detached from the body, causes most of the heating to take place in the air between the shuttle and the shock wave, and not the body of the shuttle. The air absorbs around 98% of the total heat energy generated, and the shuttle body absorbs around 2%. This spares the shuttle from burning up. Nevertheless, even with heating minimized the shuttle body can still reach a temperature of about 1600 degrees Celsius during re-entry.
The large angle of attack creates a large drag force, which in the case of the shuttle is ideal because it must slow down a great deal before landing. On the other hand, a small angle of attack will reduce the drag force but result in much higher heating of the shuttle body. We can deduce from this that sustained hypersonic flight is only feasible for very high altitudes above the earth's atmosphere, where there is virtually no air resistance. For flight within the earth's atmosphere, we wish to keep the drag force as low as possible, for fuel efficiency, and heating of the aircraft body as low as possible. For both of these criteria to be possible the maximum flight speed of an aircraft must be less than hypersonic speed.
Return to Engineering page
Return to Real World Physics Problems home page
Free Newsletter
Subscribe to my free newsletter below. In it I explore physics ideas that seem like science fiction but could become reality in the distant future. I develop these ideas with the help of AI. I will send it out a few times a month.