About me and why I created this physics website.

GPS Physics

The Global Positioning System (GPS) is used around the world as a navigational aid. It tells you where you are and how to get to where you want to go. This is made possible by 24 GPS satellites which are in high orbit, about 20,000 km above the earth. Their signaling system enables positions on earth to be calculated very accurately. Since the position calculations involve time information sent from clocks on board these satellites, these clocks must be very accurate due to the sensitive numerical nature of the calculations. The clocks used which satisfy this time accuracy requirement are called atomic clocks. They are accurate to within one billionth of a second. In addition to being very accurate these clocks also have to account for an important effect, which in physics is called relativity. Relativity is a proven concept in physics in which time passes at a different rate depending on how fast you are moving and on the strength of the gravitational field surrounding you.

To illustrate, imagine you are standing still and there is someone moving at a certain speed relative to you. In addition, this person is wearing a watch that was synchronized with yours (while both of you were standing still). If you could see this person's watch you would notice that (in your reference frame) the time ticks away more slowly than on your watch. For speeds much less than the speed of light this difference is way too small to be of importance to us. But for something like a satellite which moves at 14,000 km/h this effect must be accounted for when calculating GPS positions.

The second effect due to relativity is gravitation. Two objects that are inside two gravitational fields of different strength experience the passage of time differently. In the case of satellites, which are orbiting far above the earth, they experience the passage of time at a different rate than objects on earth. The gravitational field experienced by the satellites while in orbit (due to the mass of the earth), has less strength than the gravitational field experienced by objects located on the surface of the earth. This means that satellites, and the clocks on board these satellites, experience the passage of time at a different rate than clocks located on earth. From our reference frame on earth, the clocks on board these satellites tick faster than clocks here on earth, due to this effect. Just like before, this effect must be accounted for in order for accurate GPS position calculations to be made.

Without getting into detailed relativity calculations, it turns out that due to the first effect (the satellite speed effect), the clocks on board the orbiting GPS satellites would lose 7 microseconds a day if they were synchronized with clocks on earth before the satellites went into orbit. And due to the second effect, the clocks on board the GPS satellites would gain 45 microseconds a day, if they were similarly synchronized. Therefore the net effect is that the clocks on board the satellites would gain 45-7 = 38 microseconds a day, due to the effects of relativity. The figures below help give you a visual understanding of the differences in time between two initially synchronized clocks, for when both clocks are on earth, and after one clock goes into an orbiting GPS satellite and the other one stays on earth.





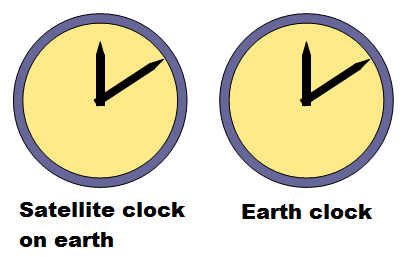
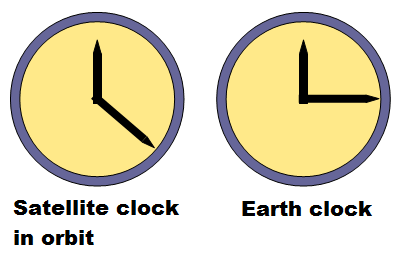
Therefore, the time measurements made with the atomic clocks on board the satellites must be adjusted in order to be used for position calculations by the GPS receivers on earth. More specifically, the clocks on board the GPS satellites must be made to tick more slowly than earth-based GPS clocks, by 38 microseconds per day, before the satellites go into orbit. Hence, when the GPS satellites go into orbit their clocks will tick at the same rate as the GPS clocks on earth, relative to the earth reference frame. This is necessary since the earth reference frame is the frame needed to make accurate GPS position calculations on earth.

In order to calculate the position of a GPS receiver (such as your phone), the signal travel time between several satellites and receiver must be known. Typically four satellites are used for this calculation, the positions of which must also be known (as they orbit the earth). Once this travel time (from each of the satellites) is known, the travel distance can be calculated using the following formula for each of the satellites: D = T×C, where D is the travel distance, T is the travel time, and C is the speed of light. The time T is calculated by subtracting the time that the signal is sent from each of the GPS satellites (given by the atomic clocks on the GPS satellites), from the time this signal is received by the GPS receiver on earth (given by the clocks inside the GPS receivers). If the GPS clocks and receiver clocks are perfectly synchronized then this time difference will precisely equal the travel time T, and this is used to calculate D for each of the satellites. From there the position of the receiver is calculated by the microcomputer inside the receiver, using trilateration equations. The accuracy of this position calculation is very accurate, usually within a few meters.

As mentioned, four satellites are typically used for position calculations, using distance measurements from these four satellites. But mathematically speaking it is only necessary to have distance measurements from three satellites to calculate position (using three corresponding equations). So using four satellites for position calculations (using four corresponding equations) is redundant from a mathematical perspective. However, since the clocks inside typical GPS receivers (such as your phone) do not have atomic clock accuracy, the fourth distance measurement (using the fourth satellite) enables an additional (fourth) equation to be used in order to more precisely calculate the receiver position. In addition, this also enables the receiver clock to be synchronized with the satellite GPS clock, using a time "correction factor" which is calculated from the four equations. By doing this the clocks inside GPS receivers do not need to have atomic clock accuracy (which would be prohibitively expensive). Instead they are constantly kept synchronized with the satellite GPS clock by applying this correction factor whenever position calculations are made.

The speed of the signals sent from GPS satellites can be affected by atmospheric interference, which slow down the signal speed so that it's slightly less than the speed of light in a vacuum. Other sources of error are the tiny variations in the atomic clock times on board the satellites, receiver error, electrical interference, and multipath error. Multipath error occurs when the signals transmitted from the satellites bounce off another object before reaching the receiver. This changes the travel distance of the signal, which makes it longer than the straight-line distance to the satellites, which is the distance that must be used in order for accurate position calculations to be made using trilateration.

Certain errors, such as from atmospheric interference, can be accounted for using what is known as differential correction. By putting a GPS receiver on the ground at a precisely known location, it can be used to calculate the error. This GPS receiver acts like a static reference point, which transmits messages containing error correction information to other GPS receivers that are in the local area, which can then use this information to correct their position calculations.

References

http://www.astronomy.ohio-state.edu/~pogge/Ast162/Unit5/gps.html
http://www.montana.edu/gps/NAVSTAR.html



Return to Physics Essays page


Return to Real World Physics Problems home page