About me and why I created this physics website.
Ferris Wheel Physics
Source: http://www.flickr.com/photos/celesteh/3266073975
Ferris wheel physics is directly related to centripetal acceleration, which results in the riders feeling "heavier" or "lighter" depending on their position on the Ferris wheel.
The Ferris wheel consists of an upright wheel with passenger gondolas (seats) attached to the rim. These gondolas can freely pivot at the support where they are connected to the Ferris wheel. As a result, the gondolas always hang downwards at all times as the Ferris wheel spins.
To analyze the Ferris wheel physics, we must first simplify the problem. The figure below shows a schematic of the Ferris wheel, illustrating the essentials of the problem.
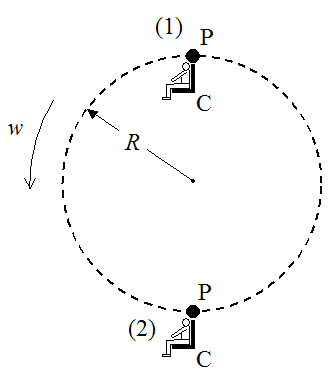
Where:
(1) is the top-most position and (2) is the bottom-most position
Point P is where the gondolas are attached to the Ferris wheel
Point C is where the passengers sit (on the gondola)
R is the radius of the Ferris wheel
w is the angular velocity of the Ferris wheel, in radians/s
The forces acting on the passengers are due to the combined effect of gravity and centripetal acceleration, caused by the rotation of the Ferris wheel with angular velocity w.
We wish to analyze the forces acting on the passengers at locations (1) and (2). The figure below shows a free-body diagram for the passengers at these locations.
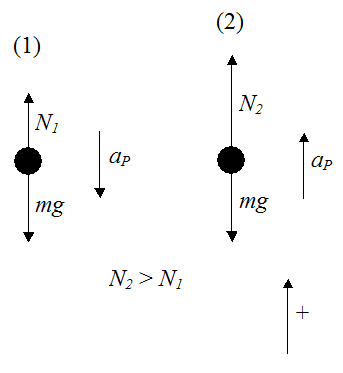
Where:
mg is the force of gravity pulling down on the passengers, where m is the mass of the passengers and g is the acceleration due to gravity, which is 9.8 m/s2
N1 is the force exerted on the passengers (by the seats) at point C, at location (1)
N2 is the force exerted on the passengers (by the seats) at point C, at location (2)
aP is the centripetal acceleration of point P. This acceleration is always pointing towards the center of the wheel. So at location (1) this acceleration is pointing directly down, and at location (2) this acceleration is pointing directly up.
The centripetal acceleration is given by
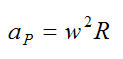
The centripetal acceleration always points towards the center of the circle. So at the bottom of the circle, aP is pointing up. At the top of the circle aP is pointing down. At these two positions aP is a vector which is aligned (parallel) with gravity, so their contributions can be directly added together.
By Newton's second law
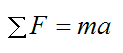
where ΣF is the sum of the forces.
To solve for N1 and N2 we must apply this equation in the vertical direction.
The acceleration of the passengers at point C is equal to the acceleration of the Ferris wheel at point P. This is because point C does not move relative to point P. Therefore, the velocity and acceleration of these two points are the same.
First, solve for N1
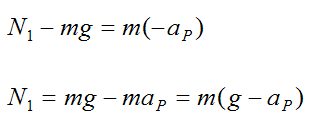
Next, solve for N2
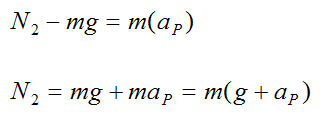
We can see that N2 > N1. This means that the passengers feel "heaviest" at the bottom of the Ferris wheel, and the "lightest" at the top.
So basically, the motion of a Ferris wheel affects your bodies "apparent" weight, which varies depending on where you are on the ride. The riders only feel their "true weight", when the centripetal acceleration is pointing horizontally and has no vector component parallel with gravity, and as a result it has no contribution in the vertical direction. This occurs when the riders are exactly halfway between the top and bottom (i.e. they are at the same height as the center of the Ferris wheel).
It's informative to look at an example to get an idea of how much force acts on the passengers.
Let's say we have a Ferris wheel with a radius of 50 meters, which makes two full revolutions per minute.
Two full revolutions per minute translates into w = 0.21 radians/s.
Substituting this into the above equations we find that
aP = 2.2 m/s2 (centripetal acceleration)
Therefore,
N1 = m(g − 2.2)
N2 = m(g + 2.2)
With g = 9.8 m/s2,
N1 = 7.6m
N2 = 12m
At the top of the Ferris wheel the passengers experience 0.78g (they feel lighter).
At the bottom of the Ferris wheel the passengers experience 1.2g (they feel heavier).
Now that we understand the physics of a Ferris wheel, one can imagine how important it is for a large radius Ferris wheel to turn slowly, given how much influence the rotation rate w will have on the centripetal acceleration aP, and on N1 and N2, as a result.
Return to Amusement Park Physics page
Return to Real World Physics Problems home page