About me and why I created this physics website.

The Difference Between Momentum And Kinetic Energy

In physics you often hear the words "momentum" and "kinetic energy". It might be tempting to think that they are fairly similar concepts, but in fact they are not. They are related concepts, but are distinct in the physical sense.

To get you thinking more deeply about this imagine getting struck by two fast moving objects having the same momentum. One object weighs 10 kg and the other object weighs 0.1 kg. Which object would inflict more damage?

The intuitive response to this might be that they would both inflict an equal amount of damage given that they both have an equal amount of momentum.

As it turns out, the 0.1 kg object would inflict much more damage. How so?

The way to understand this is to look at the mathematical representation of momentum and kinetic energy for a particle; where a particle is used as a reasonable representation for the objects.

The momentum of a particle is given by the equation, P = mv, where P is the momentum of the particle, m is the mass of the particle, and v is the velocity of the particle.

The kinetic energy of a particle is given by the equation, KE = (1/2)mv². If we substitute the equation for momentum into this equation we get,

KE = (1/2)P²/m

Since m is in the denominator, the kinetic energy is larger for a smaller m, with P held constant. Therefore, the object weighing 0.1 kg will have a lot more kinetic energy than the object weighing 10 kg, for a given momentum P. In fact, the kinetic energy of the 0.1 kg object will be 100 times greater than the kinetic energy of the 10 kg object. The kinetic energy of an object is directly proportional to how much damage it will inflict when it strikes something. But interestingly enough, it's the object weighing less that will do more damage, for a given momentum. And it is the square of the velocity in the kinetic energy equation which makes this effect possible.

You can generalize this result to say that the ratio of kinetic energy of two objects having the same momentum is the inverse ratio of their masses.

This principle readily applies to firearms. When a bullet leaves a gun it has the same momentum as the gun (which recoils), due to conservation of momentum. But the bullet has much more kinetic energy than the gun. Looking at this more deeply you realize that much more of the gunpowder energy was transferred to the bullet than the gun, in the form of kinetic energy.

As an analogy to the gun and bullet consider the figure below showing two blocks with a spring held between them. This spring represents the gunpowder which stores the energy pushing the bullet and gun apart, represented by the smaller block and larger block, respectively.



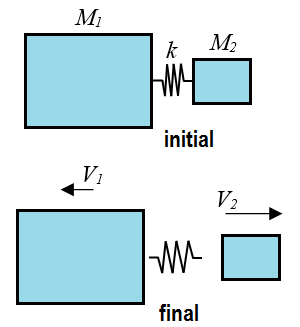
Initially, the spring is compressed between the blocks. The spring is then released and pushes the two blocks apart. In this system momentum is conserved, and as shown previously, the kinetic energy of the smaller block of mass M₂ is larger than the kinetic energy of the larger and heavier block of mass M₁. As a result, the velocity of the smaller block V₂ is greater than the velocity of the larger block V₁. Since momentum is conserved the velocities of the two blocks are related by the following equation: M₁V₁ = M₂V₂.

As a result, most of the energy of the spring goes into the smaller and lighter block. This is just the nature of the physics at work which we arrive at using mathematics. If the stiffness of the spring is k, the elastic energy of the spring when compressed is (1/2)ks², where s is the amount that the spring is compressed.

It is informative to write an equation expressing the total energy of the system. This is given by,

(1/2)ks² = (1/2)M₁V₁² + (1/2)M₂V₂²

where most of the energy goes into the smaller lighter block.

So in this case, bigger is definitely better. For two objects having the same momentum you want to be struck by the heavier object since it will inflict less damage.



Return to Physics Essays page


Return to Real World Physics Problems home page