About me and why I created this physics website.

Elastic Collision

An elastic collision is commonly defined as a collision in which linear momentum is conserved and kinetic energy is conserved. In several problems, such as the collision between billiard balls, this is a good approximation.

The general equation for conservation of linear momentum for a system of particles is:



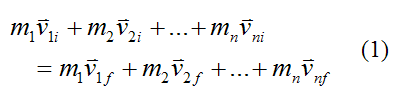
Where:

m₁, m₂,..., m_n is the mass of the individual particles in the system

v_1i, v_2i,..., v_ni is the initial velocity of the individual particles in the system, with respect to an inertial reference frame (ground)

v_1f, v_2f,..., v_nf is the final velocity of the individual particles in the system, with respect to an inertial reference frame (ground)


If the kinetic energy is conserved in the system of particles then



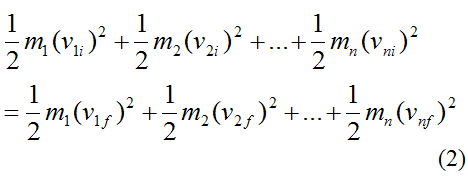
Note that the velocity terms in the above equation are the magnitude of the velocities of the individual particles, with respect to an inertial reference frame (ground).


In a collision between particles, kinetic energy is conserved if the particles behave elastically during the collisions. This means that, during impact, the particles deform elastically; meaning they behave like perfectly elastic springs, absorbing and releasing the same energy during impact.

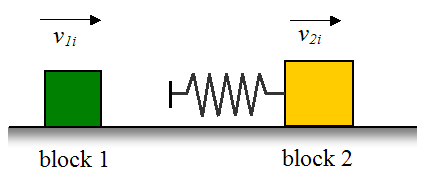
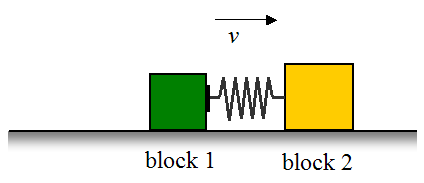
To help illustrate this concept consider the following analogy, where a spring is attached to a block, and another block collides with it. Both blocks are moving on a flat frictionless surface and no external forces are acting on the blocks in the direction of motion. The spring is a mathematical representation of the "springiness" of the particles as they collide.

There are three distinct stages:


Stage (1), before the collision: Both blocks are moving on a frictionless surface at an initial velocity.



In this stage, the total energy in the system is given by



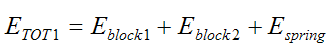
The energy of the blocks is equal to their kinetic energy. The energy of the spring is zero since it is at its equilibrium (unstretched) length.

Therefore,




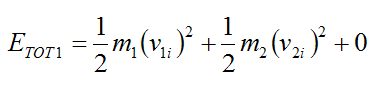
Stage (2), at the midpoint of the collision: The spring has compressed by the maximum amount and as a result is storing its maximum energy. Both blocks are moving at the same velocity v at this instant.



In this stage, the total energy in the system is given by



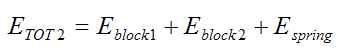
The energy of the blocks is equal to their kinetic energy. The energy of the spring is equal to its stored energy due to it being compressed.

Therefore,



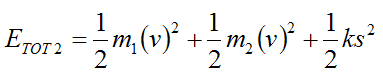
where k is the spring constant and s is the amount the spring is compressed.

Since the spring is assumed to be elastic, energy is conserved at this stage. Therefore, by the law of conservation of energy




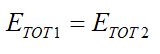
Stage (3), after the collision: The spring has released and both blocks are moving at a different velocity.



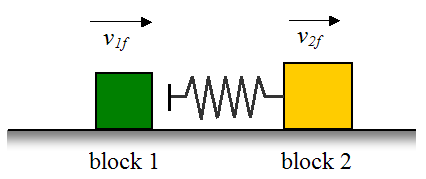
In this stage, the total energy in the system is given by



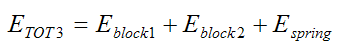
The energy of the blocks is equal to their kinetic energy. The energy of the spring is zero since it is once again at its equilibrium (unstretched) length.

Therefore,



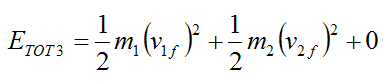
Since the spring is assumed to be elastic it has returned 100% of its energy to the system (stored during stage 2). Therefore, by the law of conservation of energy




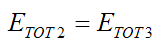
As a result,



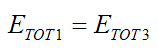
Stage 1 and stage 3 represent the initial and final states of the system, and from the above equation we can write



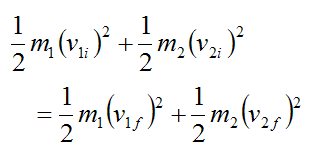
Therefore, for an elastic collision kinetic energy is conserved.


Elastic Collision Between Two Particles

General equations can be developed for the elastic collision between two particles.




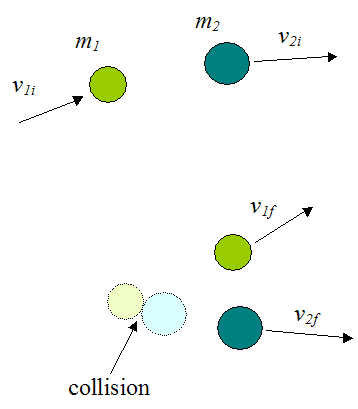
From equation (1) for the conservation of linear momentum we have



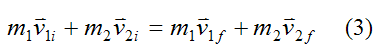
This equation can be expressed as its corresponding (scalar) equations along Cartesian x, y, z directions:



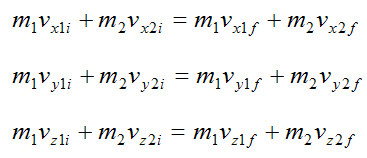
From equation (2) for the conservation of kinetic energy we have



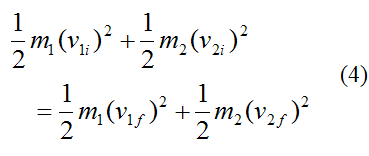
For the special case of a head on elastic collision in one dimension, we can solve equations (3) and (4) for the final velocities of the two particles:





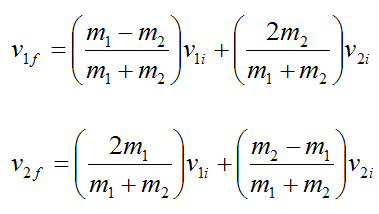
Return to Dynamics page


Return to Real World Physics Problems home page