About me and why I created this physics website.

The Physics Of Skateboarding

An understanding of the physics of skateboarding is useful to skateboarders when they do some of their tricks and jumps. It allows them to identify those key physics principles enabling them to properly execute certain moves, which is useful from a performance point of view. In addition to having an intuitive understanding gained from practice, understanding some of the physics theory behind the tricks and jumps can help make sense of the mechanics involved, which is particularly useful for those who are just starting out.

The physics behind several skateboarding tricks will be discussed.

Physics Of Skateboarding – The Hippie Jump

In the hippie jump, a skateboarder rides along on a flat horizontal surface at a certain velocity V_h. He then jumps straight up without exerting any horizontal force on the board. This allows him to fly through the air at the same horizontal velocity as the board (also moving at V_h). As a result, the board remains directly below him and he is able to land on top of it. The figure below illustrates this.



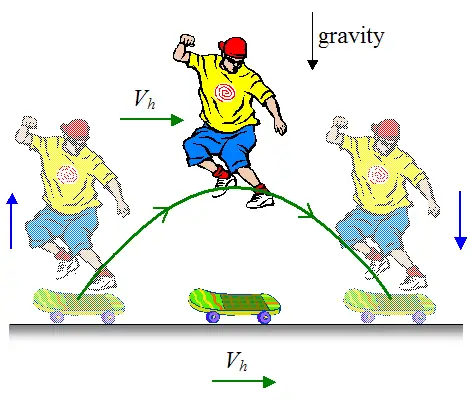
In this trick the skater must propel himself up by pushing vertically down with his legs. If he pushes on the board with even the slightest horizontal force the board will shoot out either in front of him or behind him.

After the skateboarder jumps off the board, gravity takes over and he follows a parabolic arc as he flies through the air (as shown), before landing back on the board.

The physics behind this trick can be described by the equations of projectile motion, where only the vertical component of velocity changes, since gravity only acts in the vertical direction. The horizontal component of velocity V_h of the skateboarder stays the same since there is no force acting on him in the horizontal direction (neglecting air resistance). The friction force acting on the board as it rolls along (due to contact with the ground) is small and doesn't slow the board down appreciably. As a result, its velocity is approximately the same as the horizontal velocity of the skateboarder. This allows the skateboarder to land back on the board.

To make the jump more challenging, the skateboarder can do the jump over an obstacle, as shown below.



Source: http://www.flickr.com/photos/watko/3573662093


Physics Of Skateboarding – The Ollie

The Ollie is a fundamental skateboarding trick. It is often used as the basis of other more complicated tricks. The beginning of the Ollie consists of two basic actions, occurring at roughly the same time. The first action is the skateboarder jumping up and off the board. This is accompanied by him pushing down quickly on the tail end of the board, causing it to rebound off the ground and bounce back up. The skateboarder then guides the board along with his feet as it flies through the air, enabling him to land back on top of it.

The figure below illustrates the physics of the Ollie. The arrows represent the forces acting on the board during the different stages of the trick. The red arrows represent the force exerted on the board by the skateboarder's feet. The black arrow represents the force of gravity pulling down on the board (this force is acting through the center of mass of the board). The blue arrows represent the force exerted on the board by the ground.





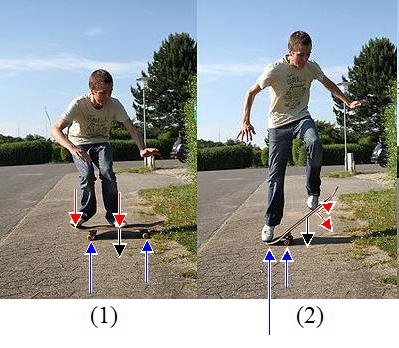
Source: http://en.wikipedia.org/wiki/Ollie_(skateboarding_trick). Author: http://en.wikipedia.org/wiki/User:TobiasK


In stage (1) of the Ollie, the skater is crouched down and is preparing to jump off the board. His right foot is on the tail of the board and his left foot is near the middle of the board. The three forces (represented by the red, black, and blue arrows) all balance out to zero in this stage since the board is stationary (with no acceleration).

In stage (2), the skater propels himself upward by explosively straightening his legs and lifting up his arms. At the same time he pushes down with his right foot much harder than with his left foot. This causes the board to tilt back and strike the ground with the tail. When the tail strikes the ground a large vertical impulse force is generated with the ground (denoted by the long blue arrow). This propels the board upward and also causes the board to rotate clockwise. He then slides his left foot to the left along the board and tilts it somewhat, allowing him to "grab" the rough surface of the board using the edge of his shoe. This enables him to guide the board along during the remainder of its motion (as it becomes airborne). The force exerted on the board by his left foot is broken down into two components (shown as perpendicular to the board, and parallel to the board). The parallel component of this force is what "drags" the board along.

In stage (3), his right foot has lost contact with the board. He is guiding the board along with his left foot, and dragging the board upward even higher.

In stage (4), he brings the board into the horizontal position by pushing down with his left foot, while raising his right foot (in order to get it out of the way of the rising tail of the board). He is now making contact with the board with both his feet and is now able to land squarely on the board.


The Ollie can also be done as the skater is rolling along on the ground at constant speed. In this case the physics of the Ollie, described in the four stages above, remains the same.


Physics Of Skateboarding – Frontside 180

The physics of the frontside 180 involves the conservation of angular momentum. In this trick the skateboarder rotates his board 180 degrees in the air so that, upon landing, he is facing in the opposite direction to before. He does this even though his initial angular momentum is zero, meaning he is not rotating initially. The figure below illustrates this trick.



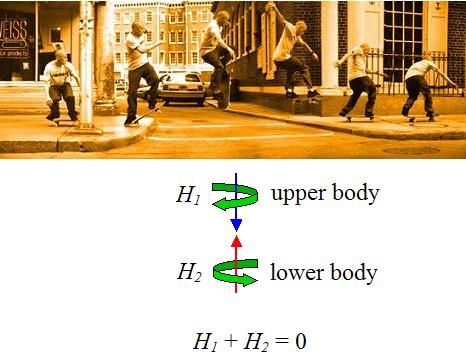
Source: http://www.exploratorium.edu/skateboarding/trick03.html. Author: http://www.exploratorium.edu (Mid-Air Maneuvers © The Exploratorium)


As the skateboarder gets airborne, the only force acting on him is gravity, which acts though the center of mass of the system (consisting of skater plus board). Because of this, the gravity force cannot exert a torque on the skater-board system. So as a whole the system cannot rotate.

So what is the physics taking place here, and how does the skater manage to rotate his board 180 degrees by the time he lands back on the ground?

He does this by rotating his upper body and lower body in opposite directions. This way he can land with the board facing the other way, while still adhering to the physical requirement that the angular momentum of the system remains zero.

As shown in the figure above, he gives his upper body a clockwise rotation, resulting in an angular momentum for his upper body equal to H₁. At the same time he gives his lower body (including the skateboard) a counterclockwise rotation, resulting in an angular momentum for his lower body (plus skateboard) equal to H₂. Since angular momentum is conserved for the system, H₁+H₂ = 0.

The key is for him to generate a high enough H₁ so that his lower body (including the skateboard) must match this value (with H₂) by rotating 180 degrees in the other direction. He does this by extending out his arms as he is airborne. This increases the rotational inertia of his upper body, which increases H₁ (since angular momentum is given by H = Iw, where I is the rotational inertia and w is the angular velocity of the body).

Once the skateboarder lands on the ground he simply rotates his upper body back around so that he now faces the wall. He is able to do this because (after landing) he is able to exert a torque against the ground, allowing him to rotate his body back around so that he is now facing entirely in the opposite direction to before.


Physics Of Skateboarding – Pumping On A Half-Pipe

Pumping on a half-pipe is used by skateboarders to increase their vertical take-off speed when they exit the pipe. This enables them to reach greater height and perform more tricks, while airborne.

The figure below shows a skateboarder approaching the curved portion of the half-pipe.



Source: http://www.flickr.com/photos/milesgehm/164988784


The figure below shows a skateboarder after he has exited the half-pipe and is airborne.



Source: http://www.flickr.com/photos/jlantzy/2229375468


The skateboarder is able to increase his speed without having to push off the ground with his feet. In other words, his feet never have to leave the board. This begs the questions; what is the physics taking place, and how does the skater increase his speed without pushing off the ground?

To increase his speed, the skateboarder crouches down in the straight part of the half-pipe (as shown in the figure above). Then when he enters the curved portion of the half-pipe he lifts his body and arms up, which results in him exiting the pipe at greater speed than he would otherwise.

The basic skateboarding physics behind this phenomenon can be understood by applying the principle of angular impulse and momentum.

The schematic in this analysis is given below.



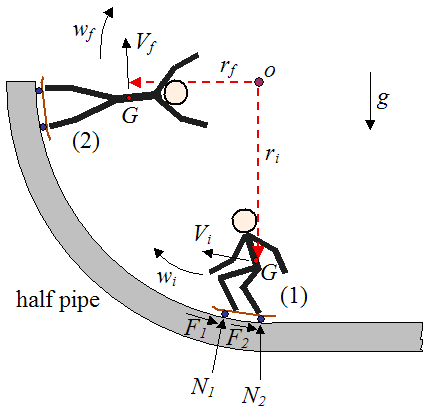
Where:

w_i is the initial angular velocity of the body (consisting of skateboarder plus board), at position (1)

w_f is the final angular velocity of the body, at position (2), which is the point at which the skater exits the half-pipe

V_i is the initial velocity of the center of mass G of the body, at position (1)

V_f is the final velocity of the center of mass G of the body, at position (2)

r_i is the initial distance from the center of rotation o to the body's center of mass G, at position (1)

r_f is the final distance from the center of rotation o to the body's center of mass G, at position (2)

g is the acceleration due to gravity

N₁ and N₂ are the normal forces acting on the wheels, as shown

F₁ and F₂ are the friction forces acting on the wheels, as shown

It is assumed that the half-pipe is a perfect circle with center at o.


The physics can be analyzed as a two-dimensional problem.

Now, apply the equation for angular impulse and momentum to the system (consisting of skateboarder plus board):



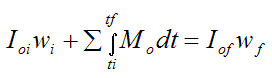
Where:

I_oi is the initial moment of inertia of the body (consisting of skateboarder plus board) about an axis passing through point o and pointing out of the page, at position (1)

I_of is the final moment of inertia of the body (consisting of skateboarder plus board) about an axis passing through point o and pointing out of the page, at position (2)

ΣM_o is the sum of the moments about point o. These moments are integrated between an initial time t_i (at position 1) and a final time t_f (at position 2)

Here we are assuming that the body can be treated as rigid at positions (1) and (2), even though the skater does in fact change his moment of inertia between these two positions. But as it turns out, when using this equation we only need to know the initial and final values of the moment of inertia of the body.

The line of action of the normal forces N₁ and N₂ pass through point o, so they do not exert a moment on the body about point o. The friction forces F₁ and F₂ are small so they can be neglected in terms of their moment contribution. This leaves only the gravitational force which exerts a moment on the body about point o. (Note that the gravitational force acts through the center of mass of the body, consisting of skateboarder plus board).

In the above equation isolate w_f. Thus,



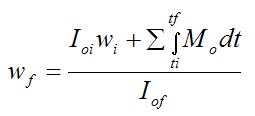
Now,



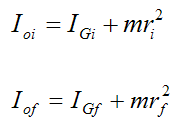
Where:

I_Gi is the initial moment of inertia of the body about an axis passing through point G and pointing out of the page, at position (1)

I_Gf is the final moment of inertia of the body about an axis passing through point G and pointing out of the page, at position (2)

m is the mass of the body


In the above equation for w_f, if we decrease I_of the angular velocity w_f will increase beyond the value it would be if we did not decrease I_of. In practice this can be accomplished by sufficiently reducing the distance from the center of mass of the body G to the point o. In other words, make r_f small enough and w_f will increase. Note also that the terms I_Gf and ΣM_o may also change somewhat. But the dominant effect will be that of reducing r_f.

At positions (1) and (2), the velocity of the center of mass G is given by



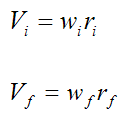
These two velocities are parallel to the half-pipe since the body is rigid at positions (1) and (2).

Looking at the above equations for velocity, if the skateboarder makes r_f small enough (by lifting his body and arms up), he will significantly increase w_f. This in turn will result in his velocity exiting the pipe (V_f) being greater than if he did not lift his body and arms up.

By continually pumping his body (by crouching down and lifting his body and arms up in the curved portion of the half-pipe), the skateboarder is able to continually increase his velocity, eventually allowing sufficient height to be reached (upon exiting the half-pipe) to perform a variety of mid-air tricks.

A more intuitive (non-mathematical) explanation of the physics taking place here is that pumping adds energy to the system in the same way that a child pumping on a swing adds energy, and results in him swinging higher. Therefore, the physics of pumping on a half-pipe is similar to the physics of pumping on a swing.

As a skateboarder lifts his arms and body up he feels resistance due to the force of centripetal acceleration which tends to push his body away from the center of rotation o. This resistance is proof that work is being done, and therefore energy is being added to the system.

If you want to see a really interesting problem related to the physics of skateboarding, check out this analysis of the effect of skateboard length on jump distance when going over a ramp. Warning, there's lots of math, so you may want to just skip to the conclusion at the end.



Return to The Physics Of Sports page


Return to Real World Physics Problems home page