About me and why I created this physics website.

The Physics Of Archery

Source: http://www.flickr.com/photos/smalltownguy22/1211984197


Physics Of Archery – Archer's Paradox

There is a very interesting physical phenomenon in the physics behind archery, known as Archer's paradox. When an arrow is released to the left (or right) of a bow its trajectory follows a path that is different from its expected trajectory (as will be explained).

The contradiction, or paradox, arises from the fact that the arrow oscillates during its release, as the string is exerting its "push" force at the rear of the arrow. As a result of this oscillation, the arrow undulates around the bow shaft, enabling it to fly in a trajectory that is in the same direction as the arrow axis at full draw. The video below shows the motion of the arrow just after release, using a high-speed camera. It only takes milliseconds for the arrow to fly past the bow.



Physics Of Archery – Analysis Of Archer's Paradox

Due to the relatively high force of the bow string acting on the arrow, it rapidly accelerates and a high-speed camera is required to capture the motion. Also, because this large force is acting in the direction of the arrow shaft, it begins to oscillate (fishtail) back and forth. This is the natural vibration the arrow experiences when subjected to a brief but large force. It's similar to hitting something with a hammer and it vibrating as a result. The force acting on the arrow is equal to the draw force as the archer pulls the string back to the release position (at full draw). This force can be in the range of 30-50 lb which is very large compared to the mass of the arrow, which is why it accelerates so rapidly (due to Newton's second law, F = ma).

Thus, the physics of archery discussed here involves more than just discussing the physics of shooting an arrow at the target. The oscillation of the arrow during the release is also discussed. In the explanation that follows, more details will be given on what occurs when the arrow is released and why it flies in the trajectory that it does.

The figure below shows the initial set up, as the archer pulls the string back and is ready to release it.





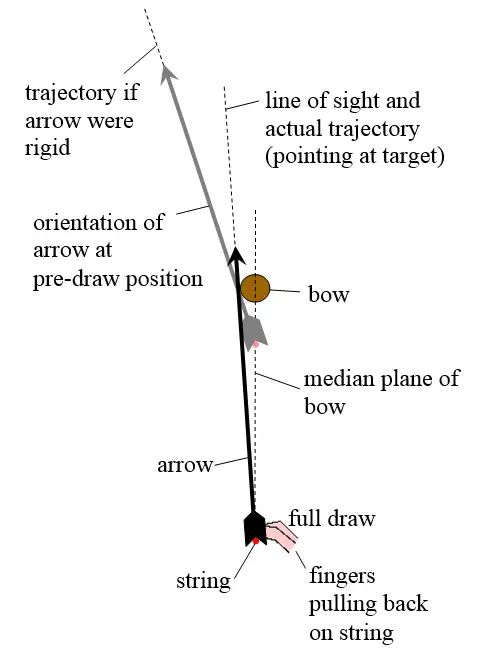
In the above figure, the line of sight used by the archer, when aiming, lies along the axis of the arrow at full draw. This is also the trajectory of the arrow after it is released. This trajectory differs from the expected trajectory the arrow would take if it were completely rigid (and did not oscillate). This expected trajectory is shown in the above figure. This expected trajectory for a rigid arrow coincides with the axis of the arrow at the pre-draw position, which is the expected (and not actual) final position of the arrow just before it exits the bow (assuming the arrow were rigid). This discrepancy between the (expected) trajectory of a rigid arrow and of the actual arrow (due to arrow oscillation) is at the heart of the archer's paradox.


First Stage of Archer's Paradox

The figure below shows the arrow immediately after release.





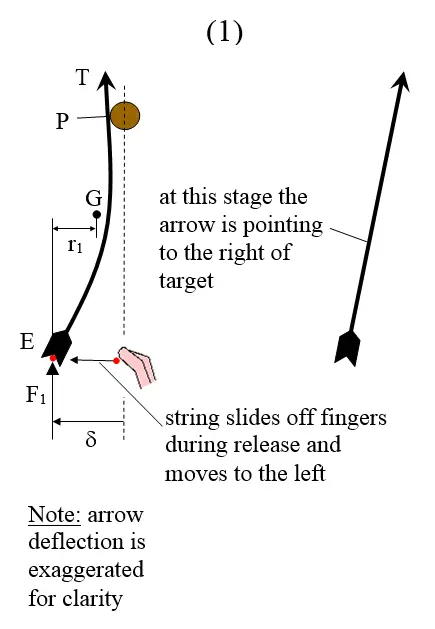
In this first stage illustrated above, three things happen:

1. As the archer opens his fingers the string slides off and moves to the left. This happens because, as the fingers open the friction between string and finger becomes insufficient to hold the string in place. So it slides off, and it does so at an angle to the median plane of the bow. This results in an initial sideways movement of the string. In reality, it would be impossible for an archer to open his fingers fast enough to prevent the string from sliding off to the side a bit, since the string moves much too quickly.

2. The leftward motion of the string excites a mode of oscillation where the arrow begins to vibrate in the plane of the page. The string force F₁ contributes to the deflection of the arrow δ beyond that due to the leftward motion of the string by itself. Note that F₁ acts in the direction of the arrow shaft.

3. The arrow is contacting the bow at point P due to a clockwise moment exerted by the string on the arrow. This moment can be taken about the center of mass G (of the arrow) at the instant shown. This moment is equal to F₁r₁, where r₁ is the moment arm F₁ makes with G. Note that this moment calculation ignores the lateral (sideways) force exerted by the string on the arrow, which is small compared to F₁.


Second Stage of Archer's Paradox

The figure below shows the arrow as it reaches the approximate halfway point past the bow.




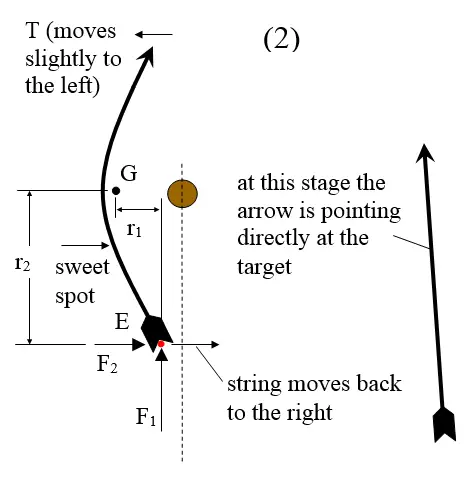
During this second stage illustrated above, two things happen:

1. The string moves to the right, as it restores its original position with the median plane of the bow. As a result, the string "pulls" on the arrow with a force F₂.

2. The tip of the arrow T moves slightly to the left. This is due to a counter-clockwise moment exerted by the string on the arrow. This moment can be taken about the center of mass G at the instant shown. This moment is equal to (F₁r₁ + F₂r₂), where r₂ is the moment arm F₂ makes with G.

The reason the tip of the arrow T moves to the left can be understood if one considers the general two-dimensional moment equation for a rigid body (taken in the plane of the page):



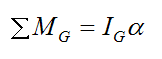
Where:

ΣM_G is the sum of the moments about the center of mass G

I_G is the moment of inertia of the arrow about the center of mass G, about an axis pointing out of the page

α is the angular acceleration of the arrow

Since the sum of the moments is counter-clockwise, α is also counter-clockwise, which means the arrow rotates counter-clockwise.

Now, the lateral motion of T (in the plane of the page) is due to two separate contributions:

(a) The counter-clockwise rotation of the arrow due to α. This causes T to move to the left.

(b) The lateral (translational) motion of the arrow due to the string pulling the rear of the arrow E to the right. Since E is below the sweet spot (shown in the figure above), movement of E to the right causes movement of T to the left. (The sweet spot is discussed in detail in The Physics Of Hitting A baseball).

Since both contributions from (a) and (b) cause T to move to the left, the resultant motion of T is to the left.

It is likely that contribution (a) is much greater than contribution (b), but for purposes of making the analysis more complete one must consider the latter contribution as well.

Note that, technically speaking, the arrow is not rigid because it's oscillating, but at the instant shown you can treat it as a rigid body.

The motion of T to the left essentially "straightens out" the path of the arrow from the first stage so that it flies along the trajectory dictated by the direction of the arrow axis at full draw.


Third Stage of Archer's Paradox

In the third and final stage illustrated below, the arrow exits the bow completely, having completed (approximately) one full oscillation. The arrow is now flying straight to the target. It will continue oscillating all the way to the target, with oscillation gradually decreasing in amplitude, but maintaining the same frequency throughout the flight.




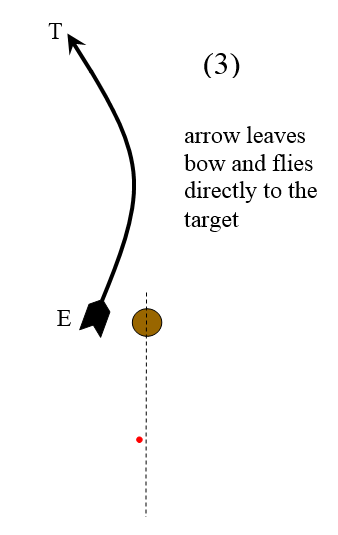
Closing Remarks

A subtle point is that, due to the induced counter-clockwise angular acceleration α of the arrow in the second stage, one might expect the arrow to keep turning counter-clockwise during the flight, causing it to "tumble" and not fly straight. However, this is not necessarily the case. The presence of vanes (fletchings) at the back of the arrow straighten it out during flight, helping it fly directly to the target. So any rotation is quickly eliminated. Fletchings aren't necessarily required but if not present then the center of pressure of the arrow has to be behind the center of mass of the arrow. This results in the aerodynamic forces straightening out the arrow during its flight. If the center of pressure of the arrow were ahead of the center of mass of the arrow it would tumble during flight. With fletchings present, the center of pressure is guaranteed to be behind the center of mass of the arrow.


In the figures above, the bow is held with the left hand and the string is released with a right-handed draw (Mediterranean release), with the arrow placed on the left of the bow. If one were to use a left-handed draw the arrow would need to be placed on the right of the bow, to create the equivalent arrow mechanics during release. So in this case the left-handed draw is a "mirror" of the right-handed draw. So the physics taking place during the release is mirrored, as well.

If one were to release the string using the thumb of the right hand (Mongolian release) the arrow would still need to be placed to the right of the bow since the string initially deflects to the right. But there is no hard and fast rule, since some archers use a variety of different techniques to obtain a straight shot.

Historical evidence of ancient arrows and bows shows that primitive archers were able to compensate (at least somewhat) for arrow oscillation during release. This is impressive considering they were not nearly as well versed in the physics of archery, as we are today.


It is important that the time it takes for the arrow to oscillate through one full cycle is approximately the time it takes for the arrow to exit the bow, after release. If the oscillation time is too slow the rear of the arrow may "slap" the bow shaft when it flies past, causing it to deflect off course and veer too far to the right. If the oscillation time is too fast, the arrow flight path may not straighten out sufficiently and it will veer to the left of the target.


The stiffness of the arrow (resistance to bending) is commonly referred to as the "spine". The stiffer the spine, the more rigid the arrow and the higher the frequency of oscillation. So the stiffness of the arrow must be just right to match the draw force of the bow, the draw length, and the archer's shooting technique. All these play an important role in determining the right choice of spine for the arrow.

It is possible to analytically predict the frequency and amplitude of oscillation of the arrow during release and model that, but it is too complicated to discuss here and won't significantly add to the basic understanding put forth here. However, great inroads have already been made in this regard, with analytical models achieving a fair degree of accuracy.

But in general, it's best to rely on the combination of analytical and empirical data already out there when determining the correct arrow to use for your bow and particular release style. And unavoidably, calibrating for the physics of archery (e.g. Archer's paradox), means one must experiment anyway to see what works best.

---

Thought Provoking Bonus Material

1. Did Hungarian archers get twice the penetration shooting a bow from a galloping horse?

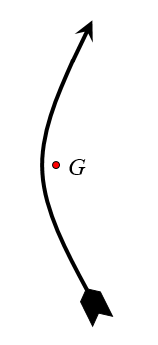
2. In archery, when an arrow is released it can oscillate during flight. If we know the location of the center of mass of the arrow (G) and the shape of the arrow at an instant as it oscillates (shown below), we can determine the location of the nodes. The nodes are the "stationary" points on the arrow as it oscillates.

Using a geometric argument (no equations), determine the location of the nodes.

Assume that the arrow oscillates in the horizontal plane, so that no external forces act on the arrow in the plane of oscillation.



I created a physics analysis for these two problems, in PDF format. It's available through this link.



Return to The Physics Of Sports page


Return to Real World Physics Problems home page