About me and why I created this physics website.

General Motion

Derivation Of General Motion Equations

A rigid body experiencing a state of general motion in three-dimensions is shown below.





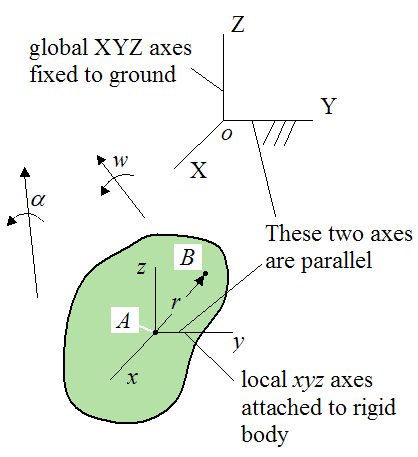
The variables in the figure are defined as follows:

A is an arbitrary point on (or in) the rigid body

B is an arbitrary point on (or in) the rigid body

w is the angular velocity of the rigid body, with respect to ground

α is the angular acceleration of the rigid body, with respect to ground

r is the position vector from point A to point B. This vector is measured relative to the local xyz axes


Both coordinate systems XYZ and xyz are defined as parallel to each other. This is done so that vector components relative to each coordinate system can be directly added together (since x is parallel to X, y is parallel to Y, and z is parallel to Z).

The first coordinate system is the global XYZ reference frame. This reference frame is defined as fixed to the ground. The point o is the origin of XYZ.

The second coordinate system is the local xyz reference frame. This reference frame is defined as attached to the rigid body and moving with it. The origin of this reference frame is located at point A.

For both coordinate systems the individual axes shown correspond to the positive directions of those axes. For example, the positive direction of the Y-axes is to the right. The positive direction of the Z-axes is up.

The choice of positive direction for these two coordinate systems is defined in this way because the equations that will be presented here involve vector cross-product multiplication, the mathematics of which is based on this choice of sign convention. So it is important to use the same sign convention when solving problems using the equations presented here. If you use another sign convention, you might get the wrong answer.


We wish to find the general motion equations for velocity and acceleration of point B, relative to the fixed (ground) reference frame XYZ.

Note that point B is not necessarily moving with the rigid body. In other words, point B could be changing position relative to the rigid body. The figure below illustrates this.




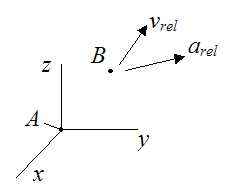
Where:

v_rel is the velocity of point B relative to the moving xyz axes. Imagine if an observer were sitting on the xyz axes. The velocity v_rel is what he would measure.

a_rel is the acceleration of point B relative to the moving xyz axes. Imagine if an observer were sitting on the xyz axes. The acceleration a_rel is what he would measure.

To find the general motion equation for the velocity of point B with respect to ground, it is useful to first imagine a simple case where point A is a stationary point (with zero velocity), and point B is attached to the rigid body and moving with it (v_rel = 0). The figure below shows the velocity of point B (v_B).

At the instant shown, the rigid body is rotating with an angular velocity w, and r is the position vector from point A to point B.

The velocity v_B is perpendicular to the angular velocity vector w and the position vector r. The magnitude of v_B is equal to |w|.|r|sinθ, where |w| is the magnitude of the angular velocity, |r| is the magnitude of the position vector, and θ is the angle between the two vectors w and r, as shown.





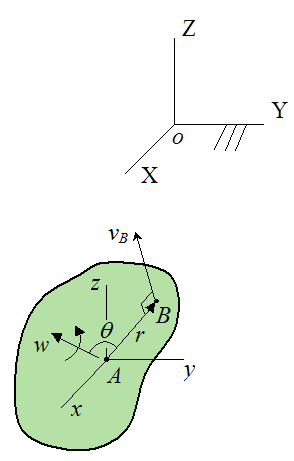
The direction and magnitude of velocity v_B is precisely given by the vector cross-product definition. Therefore,



Now, let’s say v_rel does not equal zero; which means that point B is moving relative to the xyz axes. We can account for this “extra” velocity by simply adding it to the above velocity equation. This gives us



Similarly, if point A is no longer stationary and is moving at velocity v_A with respect to ground, we can also account for it by simply adding it to the velocity equation. This gives us



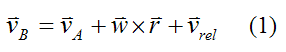
This is the most general equation for velocity of a point B (with respect to ground), on a rigid body that is translating and rotating.


To find the general motion equation for the acceleration of point B we differentiate equation (1) with respect to time. Thus,




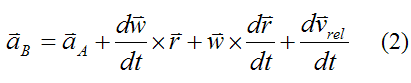
Now, by vector addition



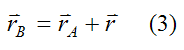
Where:

r_A is the position vector from point o (origin of the ground reference frame XYZ) to point A

r_B is the position vector from point o (origin of the ground reference frame XYZ) to point B

We can rewrite equation (3) as



Differentiate this equation with respect to time and we get



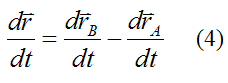
But we know that



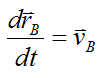
and




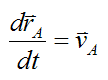
Thus, equation (4) becomes




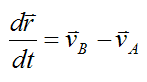
Compare this to equation (1) and we see that




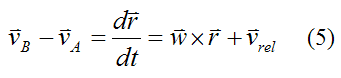
The relative velocity v_rel can be expressed as



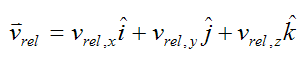
Where:

v_rel,x, v_rel,y, v_rel,z are the components of the vector v_rel relative to the local xyz axes

i, j, k are unit vectors pointing along the positive x, y, z axes (respectively)

Therefore,



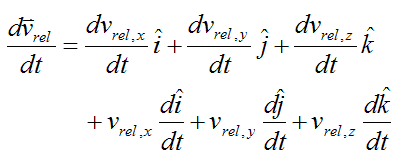
Now,



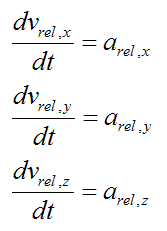
where a_rel,x, a_rel,y, a_rel,z are the components of the vector a_rel relative to the local xyz axes.


Also,




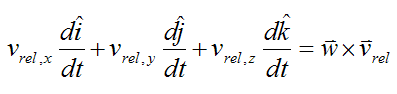
The above formulation is a result of vector differentiation. For more information about this see the page on vector derivatives.


Therefore,



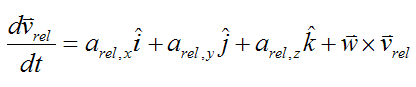
and



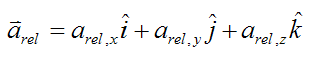
Therefore,



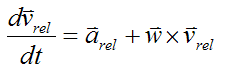
Substitute this equation and equation (5) into equation (2), and we get




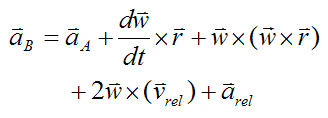
Now,




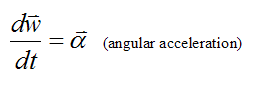
Therefore,



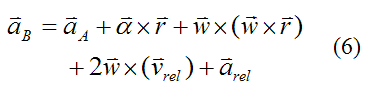
This is the most general equation for acceleration of a point B (with respect to ground), on a rigid body that is translating and rotating.


For an overview of the general motion equations click here.

To see an example of a problem solved using the general motion equations click here.


If you know the direction of spin of the angular velocity, you must use the right-hand rule to assign the correct direction for its corresponding vector, and thus determine the correct values for its three components (w_x, w_y, w_z). Similarly, if you know the direction of spin of the angular acceleration, you must use the right-hand rule to assign the correct direction for its corresponding vector, and thus determine the correct values for its three components (α_x, α_y, α_z). The right-hand rule is consistent with vector cross-product multiplication, and is therefore consistent with the choice of sign convention given here for the XYZ and xyz coordinate systems. This again stresses the importance of using the sign convention used here when solving problems using these equations. This sign convention is standard in physics books.


A Further Note On Sign Convention For General Motion Equations

As mentioned before, equations (1) and (6) (for velocity and acceleration) are based on the sign convention used here (i.e. that is how they are derived).

An example of a sign convention that does not match the one used here is shown below.





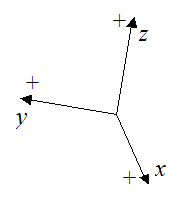
This choice of sign convention may result in errors if one uses it to solve problems using equations (1) and (6).



Return to Kinematics page


Return to Real World Physics Problems home page