About me and why I created this physics website.

Euler's Disk

Euler's disk is a fascinating physics toy. When you give it an initial spin on a smooth surface, it begins spinning and rolling (spolling) on its own.

The spolling action of Euler's disk is similar to what happens when you spin a coin on a flat surface, but it lasts much longer!

Check out a video of Euler's disk:



It's very interesting how the disk spins faster and faster as time goes on. The reason for this will be investigated.


Analysis Of Euler's Disk

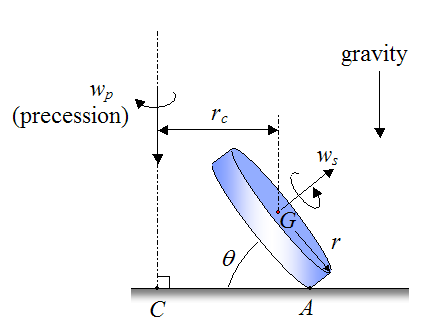
To analyze the physics of Euler's disk let's start off by drawing a schematic (shown below) which illustrates the disk spolling on a flat surface.





Where:

w_s is the rate of spin of the disk, in radians/second

w_p is the rate of precession, in radians/second

A is the contact point between the disk and the flat surface

C is the point where the axis of precession intersects the flat surface

r_c is the horizontal distance from the axis of precession to the center of mass G of the disk, as shown. It is assumed that the center of mass of the disk coincides with the geometric center of the disk.

r is the radius of the disk

θ is the angle between the horizontal and the disk


To analyze the physics of Euler's disk as simply as possible, we shall treat w_s, w_p, and θ as constant. In reality, these quantities slowly change with time (e.g. the angle θ slowly gets smaller as the disk is spolling). However, since the rate of change of these quantities is small, approximating them as constant is reasonable.

Further simplifying assumptions include:

• The disk rolls on the flat surface without slipping

• The disk is thin relative to its radius

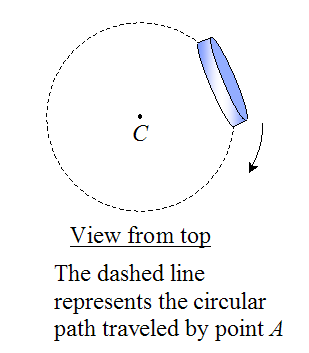
• The disk rolls such that r_c = 0. This is approximately true as θ becomes small. This means that the diameter of the circular path traveled by point A (represented by the dashed line) approaches the diameter of the disk as θ becomes smaller. You can see this is approximately true by looking at the previous video showing a spolling disk.


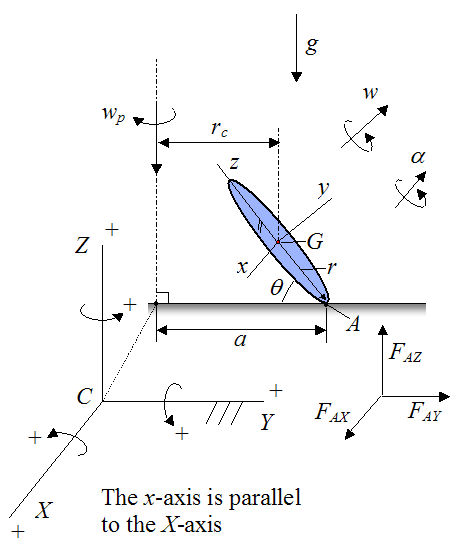
With simplifying assumptions in mind, let's now redraw the schematic. The disk is treated as "thin" such that the thickness can be neglected.



Where:

A global XYZ axes is defined as shown, with origin at point C, and fixed to ground

A local xyz axes is defined as shown, with origin at point G, and attached to the disk so that it moves with the disk. Note that this axes is aligned with the principal directions of inertia of the disk. Also note that the local x-axis is parallel to the global X-axis

g is the acceleration due to gravity

w is the angular velocity of the disk, with respect to ground

α is the angular acceleration of the disk, with respect to ground

a is the distance from point C to point A

F_AX is the force acting on the disk in the global X-direction, at point A

F_AY is the force acting on the disk in the global Y-direction, at point A

F_AZ is the force acting on the disk in the global Z-direction, at point A


Lastly, we shall define I, J, and K as unit vectors pointing along the positive directions of the global X, Y, and Z axis respectively


The angular velocity of the disk, with respect to ground, is




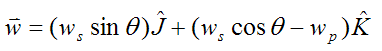
The angular acceleration of the disk, with respect to ground, is




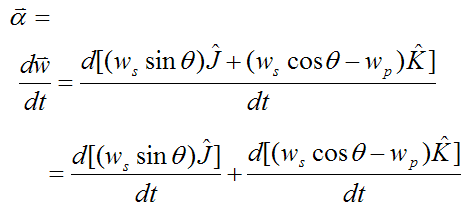
Looking at the first term:




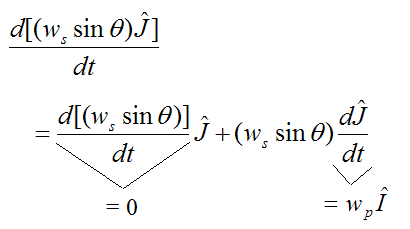
Looking at the second term:



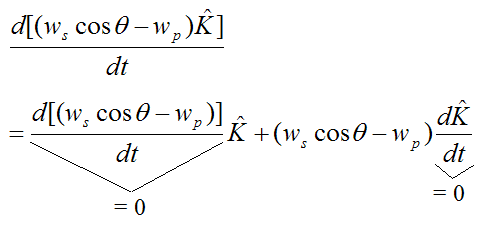
Therefore, for the disk




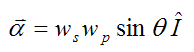
Note that the terms dJ/dt and dK/dt are calculated using vector differentiation. To learn more about it visit the vector derivative page.


For the general case of slipping between disk and surface, the velocity of point A (on the disk) is calculated by adding the linear velocity of point A due to precession (aw_p), to the linear velocity of point A due to the spin of the disk (rw_s). These two linear velocities are acting in opposite directions, so the following equation results:



where



For rolling without slipping, V_A = 0. Therefore



and



Now, for r_c = 0 we have



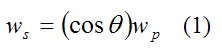
This expression conveniently relates w_s and w_p.


By Newton’s Second Law:



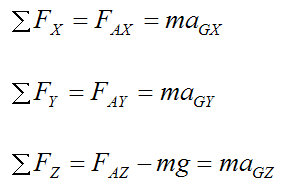
Where:

m is the mass of the disk

a_GX is the acceleration of point G in the global X-direction

a_GY is the acceleration of point G in the global Y-direction

a_GZ is the acceleration of point G in the global Z-direction


If r_c = 0 then point G is stationary, which means that the acceleration of point G is zero. Looking at the above three equations we see that they are equal to zero, as a result. This means that F_AX = 0, F_AY = 0, and F_AZ = mg.

Next, apply the Euler equations of motion for a rigid body, given that xyz is aligned with the principal directions of inertia of the disk (treated as a solid disk).

We have,



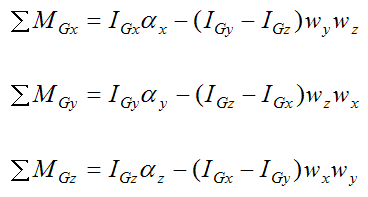
Now,



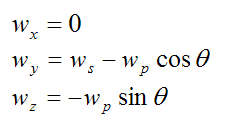
This is the angular velocity of the disk (with respect to ground) resolved along the local xyz axes.

Furthermore,



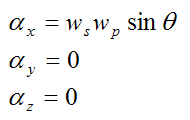
This is the angular acceleration of the disk (with respect to ground) resolved along the local xyz axes.

Thus, the second and third equations (of Euler's equations) are equal to zero. Therefore ΣM_Gy = 0 and ΣM_Gz = 0. As a result, the second and third equations do not contribute to the solution.

Therefore, we only need to consider the first equation:



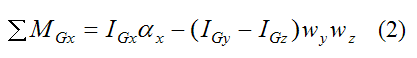
Where:

ΣM_Gx is the sum of the moments about point G, in the local x-direction.

I_Gx, I_Gy, and I_Gz are the principal moments of inertia of the disk about point G about the local x, y, and z directions (respectively).

By symmetry (treat the disk as a thin circular disk),



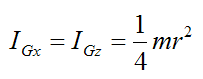
and



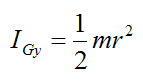
Now,



This is the sum of the moments in the x-direction about point G.

Substitute this into equation (2) and we get



Now, substitute I_Gx, I_Gy, I_Gz, α_x, w_y, w_z, and equation (1) into the above equation. We get



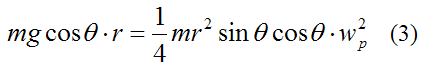
Thus,



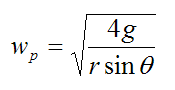
This informative result tells us that as θ→0, w_p goes to infinity. This is consistent with the rapid speed increase we see in a real Euler's disk as θ becomes small. The reason for this is because the right side of equation (3) contains a sinθ term, which goes to zero as θ→0. This means that (mathematically speaking) w_p must increase to a large value.

However, the above formula for w_p is an idealized result. In reality there is a bit of slipping (friction) at point A and some rolling resistance as well. This would affect the solution somewhat if taken into account.

As Euler's disk loses energy due to friction and rolling resistance losses, it also loses gravitational potential energy by an equal amount. This means that the center of mass G of the disk must gradually drop in height, which causes the angle θ to get smaller and smaller (as a result). This in turn causes the disk to precess faster and faster, according to the above equation. This process continues until the angle θ becomes so small that contact with the surface is inevitable and the disk is brought to a sudden halt.

Euler's disk works best when friction and rolling resistance is minimized. This is achieved on hard, low friction surfaces, such as glass.


Although the model here neglects friction, Euler's disk cannot be modeled as a conservation of angular momentum problem. This is because there is a net moment (torque) acting on the disk about its center of mass G (due to the contact force F_AZ between disk and surface, at point A).


In closing, it is worth mentioning that the physics of Euler's disk is similar to the physics of a gyroscope. Their analysis is in fact very similar.



Return to Miscellaneous Physics page


Return to Real World Physics Problems home page