About me and why I created this physics website.

Center Of Mass

A system of particles has a special point known as the center of mass. This is represented by a red dot in the figure below. The position of the center of mass is given by (x_G , y_G , z_G). The position of the individual particles of mass m_i is given by (x_i , y_i , z_i). The total mass of all the particles is M.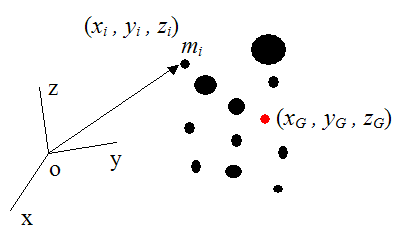





Mathematically, the position of the center of mass G is given as follows. Note that n is the number of particles in the system.





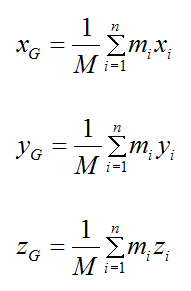
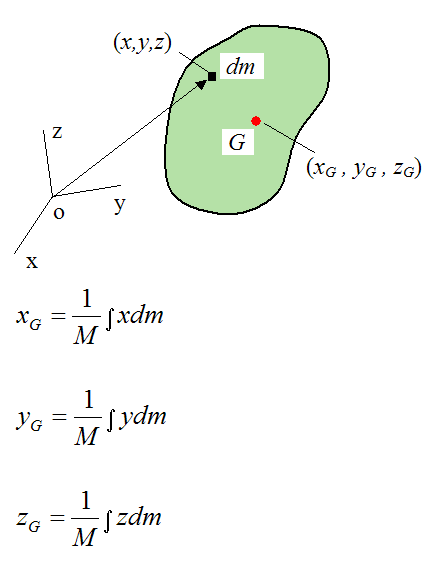
To find the center of mass of a rigid body we simply treat it as a continuous system of particles, and as such we can use the above equations (taken as integrals).

Note that the mass of the rigid body is M.





Calculating the location of the center of mass is important because it allows you to analyze dynamics problems based on the motion of the center of mass. For example, if a hammer is thrown in the air, its center of mass will follow a parabolic path. It's the same as if a particle were thrown in the air. Even though the hammer will likely rotate as it flies through the air, its center of mass will behave as a particle under the influence of gravity, so the equations for projectile motion will apply for the center of mass of the hammer.

In addition, if we have a situation where every particle within a body is subjected to the same force (such as gravity), the resultant force will act through the mass center. This is useful because it allows you to determine the moment arm of the (resultant) gravity force, depending on where you calculate your moments.


The above three equations tell us that a rigid body is "perfectly balanced" about its mass center G. So if the origin o of the coordinate frame xyz were located at point G then x_G = 0, y_G = 0, and z_G = 0.



Return to Useful Physics Formulas page


Return to Real World Physics Problems home page