The Physics Of Golf

Source: http://en.wikipedia.org/wiki/Golf. Author: http://commons.wikimedia.org/wiki/User:Lilrizz
The physics of golf is a detailed subject. It involves forces and aerodynamics, occurring during the hitting of the ball, during its flight through the air, during the run of the ball (after landing), and during the putt. Golfers often put much effort into perfecting their golf game. This effort can yield additional benefit if combined with an understanding of the physics involved. On this page, the main physics behind golf will be discussed.
The Physics Of Golf – The Golf Swing

Strobe picture taken of Bobby Jones golf swing in the 1940s. Source: http://www.clubmaker-online.com/bj003.gif
The physics of a golf swing is deceptively more complicated than one might imagine. At first glance it might appear as simple as swinging a club and hitting the ball. But in fact, there is quite a bit more to it. There is the importance of technique obviously, but there is also some interesting physics that goes into making the "perfect" golf shot.
There are two main components that go into golf swing physics. Both these will result in the best possible shot:
1. Good swinging speed of the arms and shoulders.
2. Uncocking the wrists at the right moment so that the club connects squarely with the ball. Uncocking the wrists means letting the wrists rotate freely, while still holding on to the club.
The importance of the first point is fairly obvious. You must generate good swing speed to hit the ball hard enough, so that it goes far.
The second point is not as obvious. To understand the physics of a golf swing one must consider the mechanics of rotational motion. When an object travels around in a circle it moves outward, if unconstrained. To visualize this, imagine yourself sitting in a car that makes a sharp left turn. If you're not wearing your seat belt you'll go sliding across the seat towards the right, due to the effects of centripetal acceleration.
Similarly, by uncocking your wrists during the golf swing, the club will move radially outward (since it's not restrained). This is unlike, say, baseball where the batter "drives" the bat through its arc using raw muscle power. A baseball player relies on strong wrists and forearms to get a solid hit. His hands are "active". This is unlike golf, where the players hands are "passive" since they exert no twisting force on the club. This probably gives you some idea why baseball players have such beefy forearms and wrists. They need the strength to power the bat through the swing.
Uncocking the wrists allows the golf club to "straighten out", and in the process gain additional speed which translates into a harder hit than if the golf club were held rigid (meaning the wrists are not allowed to rotate during the swing).
In the picture above, you can see the physics in action. At the top part of the swing, the golf club remains at a fixed angle relative to his arms (since his wrists are cocked). But in the bottom part of the swing, the golf club begins to "release" and the angle between it and his arms begins to rapidly increase (since his wrists are now uncocked), and the club moves radially outwards as a result. At the bottom of the swing the golf club is almost perfectly parallel to his arms. This is where contact is made with the ball.
Part of the physics of a golf swing (from the point of view of the golfer), means finding the release (wrist uncocking) point so that at the bottom position, where the players hands are directly above the ball, the golf club is in the vertical position parallel to his arms. This will maximize the speed of the club head upon impact, and result in the farthest hit.
Once the player knows the approximate point in the swing where he can uncock (release) his wrists, he just has to practice it over and over until it becomes second nature. And prior to this release point he just has to keep his wrists cocked; meaning, maintain his grip in a fixed position so that the club maintains a constant angle with his arms. Once he releases his wrists the physics takes care of the rest, and the club will move radially outwards due to the effect of centripetal acceleration.
For an in-depth physics analysis of a golf swing see Physics Of A Golf Swing.
The Physics Of Golf – Golf Club Sweet Spot
When the golf club head impacts the golf ball, it is ideal for the line of action of the impact force to pass through the center of mass of the club head. The figure below shows the center of mass of the club head (depicted by a red dot), and the point of impact (depicted by a blue dot). Note that the center of mass of the club head is actually a tiny point, which is much smaller than the red dot, whose size is greatly exaggerated for clarity.

If the line of action of the impact force (generated at the blue dot location) is overly offset from the center of mass of the club head, then we have an overly eccentric impact. As a result, the club head will excessively rotate (twist), and in addition excessive club vibration will result. It is a physics property of rigid bodies that eccentric forces, whose line of action is offset from their center of mass, create a torque which causes the body to rotate (twist).
An overly eccentric impact can cause the ball trajectory to deviate from its intended path, due to club head twist, and in addition the ball doesn't travel as far, due to energy loss from the club vibration.
The center of mass point of the club head, projected onto the club head face (in the direction that is perpendicular to the face), is commonly referred to as the "sweet spot".
If the line of action of the impact force passes through the club head center of mass, then club head twist is eliminated and vibration is minimized. But in more practical terms (which a golfer would find useful), there is perhaps an area on the club head face roughly a quarter inch wide, that contains the sweet spot, in which impact is ideal. Impact inside this area will result in minimal club head twisting and minimal club vibration.
The impact itself is a very violent event. It lasts roughly 0.0005 seconds and the force of impact can be up to 2000 pounds.
One interesting fact is that, during impact, the force exerted on the club head by the shaft is negligible compared to the impact force between club head and ball. Hence, during impact the club head can be treated as a free body. This is a very useful simplification when performing a dynamic analysis of the club head during impact.
The Physics Of Golf – Optimal Loft Angle Of Golf Club Head
It is an interesting physics problem to determine the optimal loft angle of a golf club head in order to maximize the driving distance. The loft angle is the angle between the club head face and the vertical plane, and the driving distance is the distance the ball travels through the air plus the distance it travels after it lands. The figure below shows the loft angle.
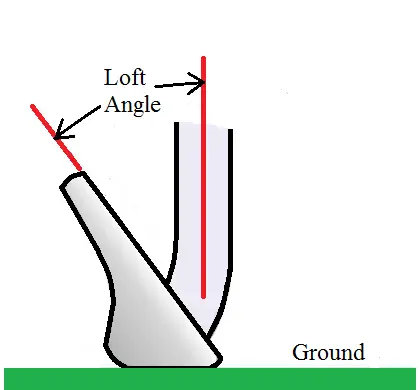
The loft angle affects the ball launch angle, the launch speed, and the rate of backspin of the ball. This in turn affects: 1) The distance the ball travels through the air, and 2) The distance the ball travels after it lands. The distance in 1) plus the distance in 2) is the driving distance. This is what we wish to maximize, based on the loft angle. This problem is tackled in the following paper:
A.R. Penner, The physics of golf: The optimum loft of a driver, Am. J. Phys. 69 (5), May 2001. http://www.raypenner.com/golf-loft.pdf
The author finds that, the greater the club head speed, the lower the optimal dynamic loft angle. The dynamic loft angle is the loft angle of the club face during impact. The dynamic loft angle, in general, is not equal to the club face loft angle when the club head is at rest on the ground – this is the angle which is typically specified on the golf club. The difference between the two angles is due to the flexing of the golf club shaft during impact. Initially, at the top of the swing, the shaft bends back causing the club head to lag behind. This is due to the inertia of the club head. However, at some point during the swing the club head catches up. But the shaft, continuing to flex, begins to flex forward. As a result, when impact occurs the club head is turned several degrees ahead of the position it would have had if the shaft had not flexed. According to the author, the dynamic loft angle will generally be several degrees greater than the loft angle when the club head is at rest on the ground.
The author determines that for initial club head speeds of 35, 45, and 55 m/s, the optimal dynamic loft angles are 16.5°, 13.1°, and 10.7°, respectively. He states that the dependence of the optimal loft angles on club head speed agrees, in general, with current practices in golf. According to his simulation results, these initial club head speeds correspond to a (maximum) driving distance of 155 meters, 210 meters, and 255 meters, respectively.
Here's a related paper by the same author:
A.R. Penner, The physics of golf: The convex face of a driver, Am. J. Phys. 69 (10), October 2001. http://www.raypenner.com/golf-convex.pdf
The Physics Of Golf – Aerodynamics Of Ball Flight
The dimples on a golf ball create a thin turbulent boundary layer of air over the ball's surface. This reduces air resistance which results in the ball traveling a farther distance than a smooth ball would. Such a distance improvement is desirable for making a shot as long as possible. The figure below shows the flow of air over a dimpled golf ball.

The air flow over the ball follows smooth streamlines until some point beyond the halfway distance, at which the turbulent boundary layer "separates" and turbulent eddies form inside a resulting wake region. This wake region has lower pressure, which causes the (greater) pressure in front of the ball to exert a net pressure force opposite the direction of motion of the ball (known as drag). Turbulent flow, induced by the dimples, reduces the size of this lower pressure wake region (from that of a smooth ball). This results in a lower net pressure force, which results in less drag than with a smooth ball. A smooth ball with no dimples would cause the boundary layer to separate sooner resulting in a larger wake region, and hence more drag would result.
The number of dimples on a typical golf ball ranges from 250-450. Different manufacturers have different theories on the ideal number of dimples, the ideal depth of the dimples, and the ideal placement pattern of the dimples. In fact, all these attributes affect the balls overall aerodynamic qualities during flight.
The figure below shows the air flow over a rotating golf ball, which experiences an upward lift force F as a result of the rotation. The ball typically rotates at several thousand RPM. (Note: This rotation is a result of the friction between club head face and ball, which causes the ball to roll up the lofted club head face during impact and gain backspin as a result).
The upward force F is caused by the Magnus effect which causes the ball to fly higher and remain airborne longer. Hence, it flies farther than it would than if there were no rotation. This, in combination with lower air drag due to the ball dimples, results in an extra long shot. In addition to greatly reducing air drag, dimples also greatly enhance the Magnus effect, resulting in a great improvement in hitting distance. For example, a dimpled ball can be driven 250 meters by a skilled golfer, as opposed to only 100 meters or so for a smooth ball (without dimples).
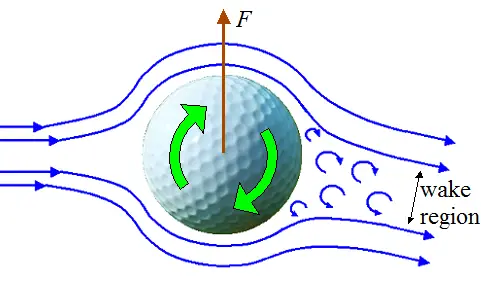
Similar to before, the air flow over the rotating ball follows smooth streamlines until some point beyond the halfway distance, at which the turbulent boundary layer separates and turbulent eddies form inside a resulting wake region. But the wake region is shifted down from before (for a non-rotating ball). The aerodynamic forces acting on the ball are thus altered. The phenomenon behind this is called the Magnus effect, and is explained below.
The figure below illustrates the Magnus effect for a rotating ball.
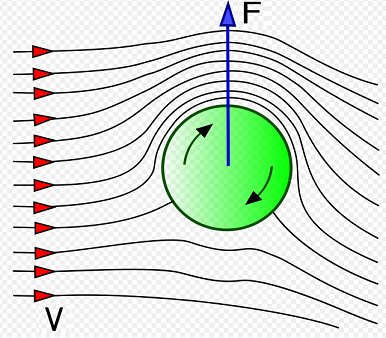
Source: http://en.wikipedia.org/wiki/Magnus_effect. Author: http://en.wikipedia.org/wiki/User:Gang65
As the ball spins, friction between the ball and air causes the air to react to the direction of spin of the ball.
As the ball undergoes backspin (shown as clockwise rotation in the figure), it causes the velocity of the air around the bottom half of the ball to become less than the air velocity around the top half of the ball. This is because the tangential velocity of the ball in the bottom half acts in the opposite direction to the airflow, and the tangential velocity of the ball in the top half acts in the same direction as the airflow. In the figure shown, the airflow is in the rightward direction, relative to the ball.
Since the (resultant) air speed around the bottom half of the ball is less than the air speed around the top half of the ball, the pressure is greater on the bottom of the ball. This causes a net upward force (F) to act on the ball. This is due to Bernoulli's principle which states that when air velocity decreases, air pressure increases (and vice-versa).
The Physics Of Golf – Putting
Lastly, we have putting, which is the gentle final shot (or set of shots) for hitting the ball into the hole. If the ground in the direction of the shot is perfectly flat, perfectly uphill, or perfectly downhill, then hitting the ball into the hole is simply a matter of hitting it along a straight line, directly into the hole.
However, sometimes the ground is sloped such that the ball trajectory cannot be a straight line in order to enter the hole. In this instance hitting the ball into the hole is a much more complicated matter. The ball must follow a precise curved path in order to enter the hole. This is shown in the figure below.

Source: http://commons.wikimedia.org/wiki/File:John_Parry_Round_3_Open_de_France_2013_t124411.jpg. Author: http://commons.wikimedia.org/wiki/User:Jastrow
The ball must roll along a curved trajectory before it can enter the hole. Whether the ball must curve left or right depends on which way the ground slope is tilting. It is evident that such a shot takes a lot of practice to master.
Modeling the mathematics of the ball trajectory on sloped ground is a complex task requiring knowledge of the ground topology (in order to properly account for the gravity force acting on the ball as it rolls along), and the dynamics of the grass-ball interaction as the ball rolls along. This is quite complicated and such an analysis will likely be of little benefit to the golfer, since this is primarily a learned skill, based on muscle memory, coordination, and human judgement.
Return to The Physics Of Sports page
Return to Real World Physics Problems home page
Free Newsletter
Subscribe to my free newsletter below. In it I explore physics ideas that seem like science fiction but could become reality in the distant future. I develop these ideas with the help of AI. I will send it out a few times a month.