About me and why I created this physics website.

Euler Force

In the presence of angular acceleration, there can exist a fictitious force known as the Euler force. This force is observed from a non-inertial reference frame.

To illustrate this concept, consider a particle P that is firmly sitting on a turntable, which is rotating about point O with a (counterclockwise) angular acceleration α. The radius measured from point O to the location of the particle is R.




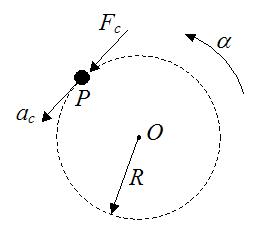
The tangential (circumferential) acceleration of the particle (a_c) is:



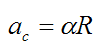
The tangential force (F_c) between the particle and turntable is preventing the particle from sliding in the circumferential direction. This force is determined by applying Newton’s Second Law in the direction of a_c.

Thus,



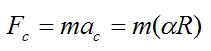
where m is the mass of the particle.


Now, let’s say the force F_c = 0. In this situation the particle would slide in the direction opposite a_c shown in the figure above. This can be deduced from Newton’s Second Law. Setting F_c = 0, it follows that a_c = 0.

Since Newton’s Second Law applies to an inertial reference frame, this means that for F_c = 0 the particle must have zero tangential acceleration relative to ground (which serves as the inertial reference frame). Thus, relative to a (non-inertial) reference frame attached to the turntable (and moving with it), the particle must move in the circumferential (clockwise) direction opposite the direction of a_c, shown in the figure above.

From the point of view of an observer sitting on the turntable (and moving with it), the Euler force is the apparent force that appears to be acting on the particle, pushing it in the circumferential (clockwise) direction. The line of action of this apparent force is therefore in the circumferential (tangential) direction and (as a result) is perpendicular to the line passing through point O and point P. But in reality, there is no actual force acting on the particle. What the observer sees is just a direct result of Newton’s Second Law, which applies to an inertial reference frame (ground). The figure below illustrates this.




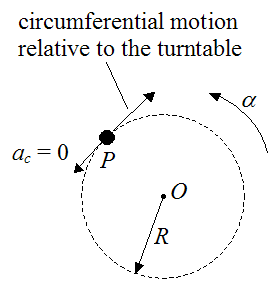
The particle will also move in the circumferential (clockwise) direction relative to the turntable, if the force F_c is insufficient to hold the particle in place. In other words,




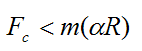
It is worth noting that, if the turntable has angular velocity, two more fictitious forces can arise. They are the Coriolis force, and the Centrifugal force.



Return to Dynamics page


Return to Real World Physics Problems home page