About me and why I created this physics website.
The Physics Of Scale
Imagine that you are looking at two identical solid spheres approaching each other head on. And let's say that you are positioned at some unknown distance from them and have no reference points with which to infer the size of the spheres. The only thing you know is that they are approaching each other and will eventually collide. The figure below shows the two spheres.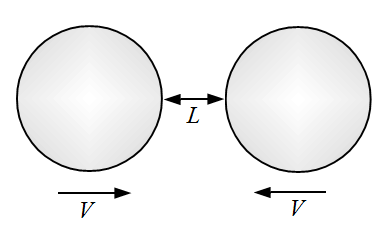
Let's say that the distance between the spheres is initially some value L which, according to the figure, is about half of the diameter of the spheres. Let's also say that their approach velocity is some value V, which is such that the distance L between the spheres reduces to zero after 1 second. This means that they impact after 1 second. This certainly gives you more information, but unless you know the actual sizes of the two spheres it is impossible for you to estimate L and V.
Now what will happen when the spheres collide?
It turns out that what will happen depends heavily on how large the spheres are. You can say a lot about the sizes of the two spheres based on what happens when they collide.
If the spheres bounce off each other with no apparent damage, due to the impact, then you can say that the spheres are fairly small. They are probably the size of small rocks or even boulders.
But if the spheres annihilate each other upon impact and a huge fireball is created then you can say that the spheres are very large, perhaps several kilometers in diameter at least.
So why should there be any difference between spheres colliding when they are the size of rocks or boulders and when they are several kilometers, or more, in size?
It's because of the fact that certain quantities, such as kinetic energy, do not scale proportionally as the mass of an object increases. The kinetic energy of an object is (1/2)MV2, where M is the mass of the object and V is the velocity of the object. The kinetic energy per unit mass then becomes (1/2)V2.
If the diameter of the spheres is, say, 1 meter, and the distance L = 0.5 meters, then V = 0.25 meters/second. Therefore the kinetic energy per unit mass is equal to (1/2)×(0.25)2 = 0.031 joules/kg.
Now if the diameter of the spheres is, say, 10000 meters, and the distance L = 5000 meters, then V = 2500 meters/second. Therefore the kinetic energy per unit mass is equal to (1/2)×(2500)2 = 3125000 joules/kg. This is much, much greater than 0.031 joules/kg! So when the 10000 meter diameter spheres collide they absorb proportionally much more energy than the 1 meter diameter spheres, even though they are colliding at the same relative velocity in a proportional sense, in that they both cover a distance equal to a quarter of their diameter in one second, before colliding.
This is why asteroids moving at 10-20 kilometers per second do so much damage if they strike the earth. They carry so much energy due to the V2 term in the kinetic energy equation. At this high speed the material strength of the colliding objects cannot withstand the immense impact energy and as a result utter and complete destruction occurs.
Another interesting consequence of scale is the time it takes for a heated object to cool depending on its size. Let's imagine we have a solid steel sphere, shown below, with diameter D.
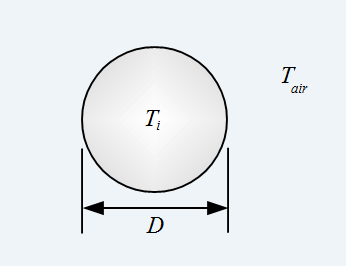
Let's say this sphere is initially heated to a uniform temperature (all the way through) of Ti = 1000 degrees Celsius. And let's further say that the sphere is allowed to cool in air which has a temperature of Tair = 25 degrees Celsius. How long will it take for the sphere to cool down completely (all the way through) to 25 degrees Celsius?
If the diameter of the sphere is, say, 1 meter, the cooling time is about 3 days.
Now what is the cooling time if the diameter of the sphere is 1000 meters?
Any guesses?
The cooling time would be about 800 years!
That's right, it would take hundreds of years for the sphere to cool down. That is another important consequence of scale. The bigger an object is the longer it takes to cool down (as well as heat up). The more intuitive reason for this is because the ratio of surface area to volume decreases the larger an object is, which means the slower it cools down, since heat loss occurs at the surface, and the less surface area there is relative to the volume, the longer the object takes to cool. This also explains why very large objects, such as planets thousands of kilometers across, take millions and even billions of years to cool down from their very hot molten state when they initially formed. And even then, only their outer layers are cooled. The core interior can still be very hot, since it is the part that cools last.
Return to Physics Essays page
Return to Real World Physics Problems home page