About me and why I created this physics website.

The Physics Of Bungee Jumping

Source: http://www.flickr.com/photos/matt-dinnery/3849606743

The physics of bungee jumping is an interesting subject of analysis. The basic physics behind this activity is self-evident. The bungee jumper jumps off a tall structure such as a bridge or crane and then falls vertically downward until the elastic bungee cord slows his descent to a stop, before pulling him back up. The jumper then oscillates up and down until all the energy is dissipated.

However, what is particularly interesting in the following analysis of the physics of bungee jumping is that the jumper experiences a downward acceleration that exceeds free-fall acceleration due to gravity. This takes place in the initial part of the fall while the bungee cord is slack (i.e. not stretched). The physics taking place here will be examined next.


Free-Fall Acceleration Greater Than g

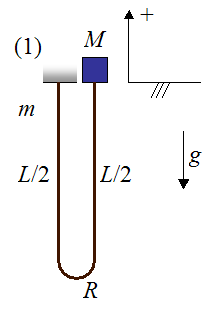
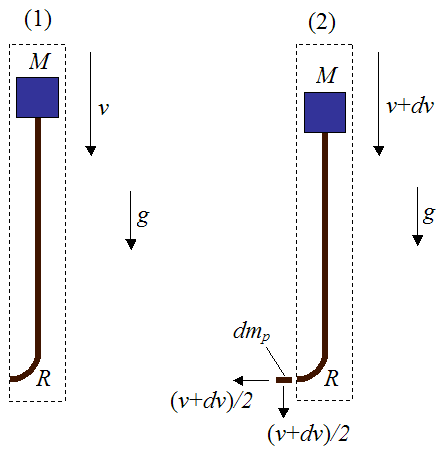
The following schematic for this analysis shows a simplified representation of a bungee jumper and bungee cord, at the initial position (1), before he jumps. The jumper is represented as a point object of mass M. The bungee cord is represented by two lengths of rope, each with length L/2, with a bend at the bottom of radius R. The left side of the bungee cord is attached to a fixed support. The mass of the bungee cord is m. The acceleration due to gravity is g (equal to 9.8 m/s² on earth). The sign convention is "up" as positive and "down" as negative.

Additional assumptions in this analysis are:

• The jumper M falls vertically downward during the fall, and the falling part of the bungee cord remains directly below him during the initial part of the fall where the bungee cord is slack.

• Friction and air resistance can be neglected.

• The radius R of the bend is small relative to the length of the straight sections of the bungee cord. Thus, the length of the bungee cord is approximately L.

• During the initial part of the fall, the extra stretching that occurs in the hanging part of the bungee cord as it supports more of its own weight, is negligible. This means that the change in elastic potential energy of the hanging part of the bungee cord (the left side of the cord in the two figures below) is small enough to be neglected in the conservation of energy equation. This is equation (1) in the analysis given below.





The following schematic for this analysis shows a representation of the bungee jumper and bungee cord after he jumps. This is denoted as position (2). The position of jumper and cord is set as a function of y which is the position of the jumper M relative to the datum (chosen as his original vertical position). The lengths of the straight sections of the cord are given as a function of y, and are based on the geometry of the problem. The vertical velocity of the jumper is given as v, and the vertical acceleration is given as a. By geometry, the vertical velocity of the bottom tip of the bend is v/2, and the vertical acceleration of the bottom tip of the bend is a/2.





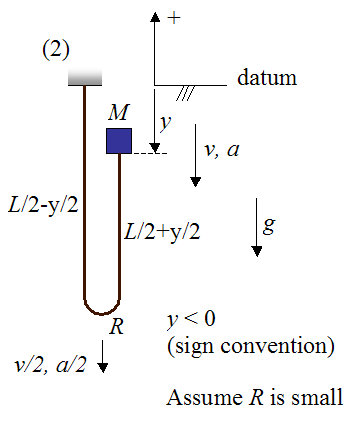
Since friction and air resistance are neglected, the physics occurring between positions (1) and (2) can be analyzed using conservation of energy for the system, which consists of bungee jumper and bungee cord. This will allow us to determine the velocity v of the jumper as a function of y. Since friction and air resistance are neglected, the only force that does work on the system is gravity.

The equation for conservation of energy is given as follows:



Where:

T₁ is the kinetic energy of the bungee jumper and bungee cord, at position (1)

V₁ is the gravitational potential energy of the bungee jumper and bungee cord, at position (1)

T₂ is the kinetic energy of the bungee jumper and bungee cord, at position (2)

V₂ is the gravitational potential energy of the bungee jumper and bungee cord, at position (2)


Since the system is at rest at position (1) the kinetic energy is



The gravitational potential energy of the system at position (1) is given by the weight of the bungee cord (mg) multiplied by the vertical position of its center of mass, as measured from the datum. (Note that the bungee cord is assumed to have uniform density, so the center of mass lies at its midpoint).

The bungee jumper M has zero gravitational potential energy because he is located at the same height as the datum.

Thus,



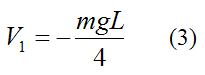
Note that this value is negative because the center of mass of the bungee cord is below the datum.

For convenience set the density of the bungee cord as ρ which is defined as mass per unit length. This is given by



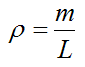
The kinetic energy of the system at position (2) is



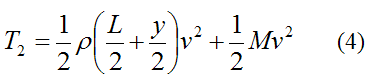
The first term on the right is the kinetic energy of the straight section of bungee cord below the jumper (M). This section of cord is moving at velocity v. The second term on the right is the kinetic energy of the jumper M, who is also moving at velocity v.

The gravitational potential energy of the system at position (2) is given by



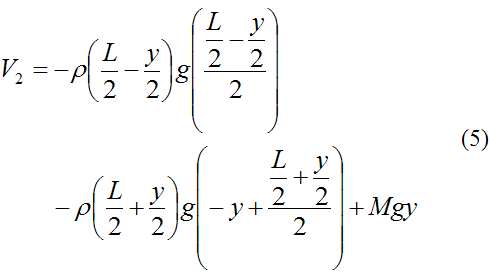
Once again, keep in mind that we are ignoring the relatively small mass of bungee cord at the bottom of the bend. Therefore this mass does not show up in the expressions for kinetic and potential energy given above.

Substitute equations (2)-(5) into equation (1) and solve for v. We get



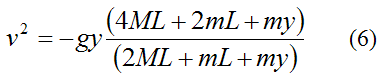
This expression conveniently relates the velocity v of the bungee jumper to his vertical position y. Once again, keep in mind that y < 0 according to the sign convention used.

The next step in this analysis is to apply the principle of impulse and momentum to solve for the acceleration of the bungee jumper (a).

To set up this analysis we shall isolate part of the system using a control volume type of analysis, which encloses the part of the system (consisting of mass M and bungee cord) that we wish to analyze. This fixed control volume is cleverly chosen in order to more easily determine the acceleration a of the bungee jumper, as he falls.



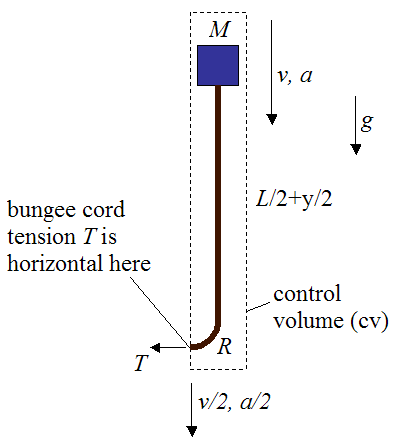
In this chosen control volume the bungee cord can be imagined as "flowing" across the system boundary (represented by the dashed line) at the lowest part of the bend, where the bungee cord tension is horizontal. The vertical component of force at this location is assumed to be very small, which is a good assumption for ropes and rope-like structures.

Since only the vertical forces acting on this system (enclosed by the control volume) will affect a, the tension T does not need to be known. This saves computation time.

The vertical force acting on the system enclosed in the control volume is gravity, which can easily be accounted for.

The next step in this analysis is to use Calculus to set up the governing equations.

Consider the figure below. The two stages, (1) and (2), show the "state" of the system at time t and time t+dt, where dt is a very small (infinitesimal) time step.

Once again, we are ignoring the mass of the rope segment of radius R at the bottom of the bend.



Between (1) and (2), the change in linear momentum in the y-direction of all the particles in the system (defined by the control volume), is due to the sum of the external forces in the y-direction acting on all the particles in the system.

We can express this mathematically using Calculus and the principle of impulse and momentum:



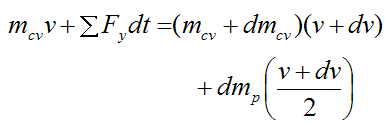
Where:

m_cv is the mass of the particles inside the control volume, at stage (1)

ΣF_y is the sum of the external forces in the y-direction acting on all the particles in the control volume

dm_cv is the change in the mass of the particles inside the control volume, between (1) and (2). Note that dm_cv < 0 since the mass of the particles inside the control volume is decreasing.

dm_p is the mass of the particles that have "flowed" to the outside of the control volume

dv is the change in vertical velocity of the particles inside the control volume, between (1) and (2). Note that (ignoring the bend) all the particles inside the control volume move at the same vertical velocity


Expand the above expression. In the limit as dt→0 we may neglect the two "second-order" terms dm_cvdv and dm_pdv/2. Divide by dt and simplify. We get



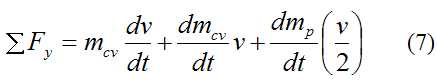
Now, the mass of the particles flowing out of the control volume must be a positive quantity. Therefore,



This means that



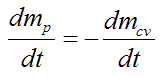
Substitute the above equation into equation (7) and we get



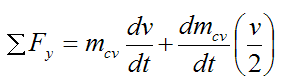
Now,



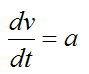
Substitute this into the previous equation and we get



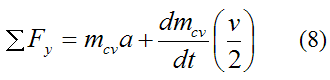
Now,



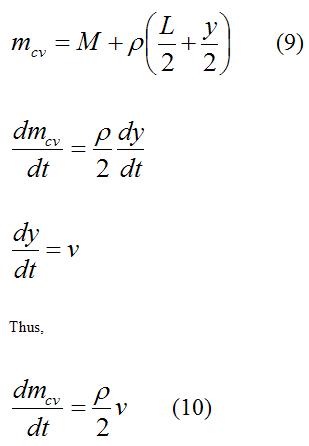
The sum of the external forces in the y-direction acting on the particles of the control volume is the gravitational force. This is given by



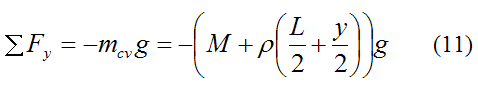
Substitute equations (9)-(11) into equation (8) and we get




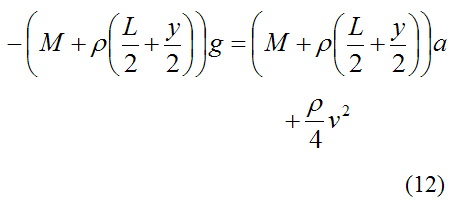
Solve for a. This gives us



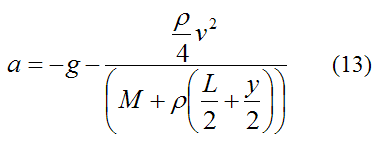
As you can see, the acceleration a is greater than g.

Note that this equation is only valid between y = 0 and y = -L.

To get an expression for a in terms of y substitute equation (6) into equation (13). This gives us



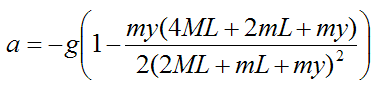
Once again, y < 0 as defined in the sign convention.

For convenience set μ = m/M. The above equation then becomes



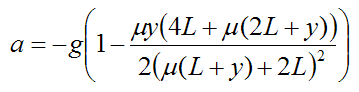
The position y = -L is the point where acceleration a is maximum. For example, if the bungee cord weighs the same as the bungee jumper the maximum acceleration is approximately 1.6g.

If we substitute a = d²y/dt² into the above equation we obtain an ordinary differential equation which we can solve numerically to determine y as a function of time. The solution is subject to the initial conditions at time t = 0. These initial conditions are: y = 0 and dy/dt = v = 0 (the system begins falling from rest).

Even though this analysis is simplified, the result that a > g makes sense because the change of velocity (from v to v/2) of the bungee cord as it travels around the bend means that there must be tension in the cord that "pulls" upward. This tension decelerates the cord at the bend location. This pull in turn, causes the segment of cord above the bend, and the jumper, to accelerate downwards faster than g.

In the final analysis let's look at the maximum distance the bungee jumper falls.


Maximum Falling Distance

Once the bungee jumper falls a distance y = -L, the bungee cord loses slack and tightens. This forceful transition is a form of inelastic collision between bungee jumper and cord, and must therefore be accounted for in this analysis in order to make accurate predictions. To solve for the velocity of the jumper immediately after the cord pulls tight, one needs to experimentally determine how much energy is lost during the "collision". Once this new velocity is calculated, the conservation of energy can once more be applied in order to determine the maximum falling distance of the jumper.

However, for illustrative purposes this energy loss will be ignored, and we shall apply conservation of energy to determine how far the bungee jumper falls, based on his initial position before jumping.

This analysis is set up using the schematic shown below. Once more we are ignoring friction, air resistance, and the relatively small mass of bungee cord at the bottom of the bend.



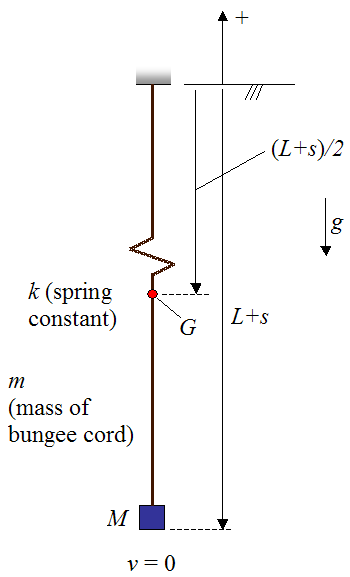
Where:

L is the (unstretched) length of the bungee cord

s is the amount the bungee cord has stretched

G is the center of mass of the bungee cord

k is the spring constant of the bungee cord, which is assumed to behave as a linear elastic spring


The maximum distance the bungee jumper falls corresponds to the lowest point in the fall, where the velocity of the system is zero. This means that the kinetic energy of the system at the lowest point is zero.

Thus, we can set up the conservation of energy equations for the system, similar to before, where position (1) corresponds to the initial (rest) position and position (2) corresponds to the lowest point in the fall (where kinetic energy is zero). The only extra consideration is that we must also account for the potential energy of the bungee cord as it stretches.

Now,



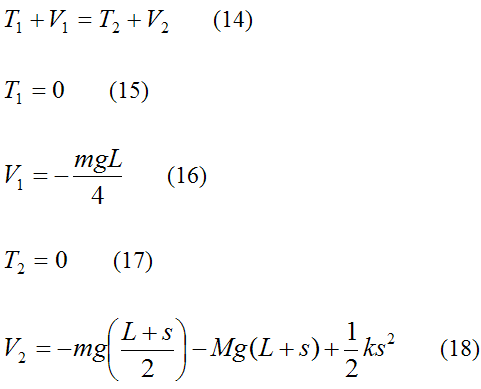
Note that the last term in the above equation represents the potential energy of the bungee cord, which is assumed to behave as a linear elastic spring.

Substitute equations (15)-(18) into equation (14). You can then solve for s numerically or with the quadratic roots formula.

For example, if k = 500 N/m, L = 15 m, g = 9.8 m/s², and m = M = 60 kg, the amount of stretch of the bungee cord is s = 8.6 m. Now, since some energy is actually lost when the bungee cord loses slack and pulls tight, this amount of stretch is a bit higher than it would be in real life.

This concludes the bungee jumping physics analysis.



Return to The Physics Of Sports page


Return to Real World Physics Problems home page