About me and why I created this physics website.

Inelastic Collision

An inelastic collision is commonly defined as a collision in which linear momentum is conserved, but kinetic energy is not conserved.

The general equation for conservation of linear momentum for a system of particles is:



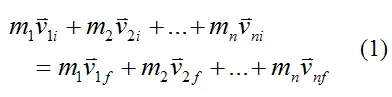
Where:

m₁, m₂,..., m_n is the mass of the individual particles in the system

v_1i, v_2i,..., v_ni is the initial velocity of the individual particles in the system, with respect to an inertial reference frame (ground)

v_1f, v_2f,..., v_nf is the final velocity of the individual particles in the system, with respect to an inertial reference frame (ground)


In an inelastic collision between particles, the particles do not behave elastically during the collision. This means that, at the point of impact, the particles do not deform elastically; meaning they may permanently deform, resulting in energy loss during impact. This is unlike an elastic collision where, at the point of impact, the particles deform elastically; meaning they behave like perfectly elastic springs, absorbing and releasing the same amount of energy during impact.

Inelastic Collision Between Two Particles

General equations can be developed for the inelastic collision between two particles.



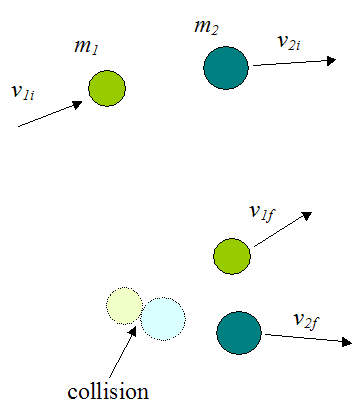
From equation (1) for the conservation of linear momentum we have



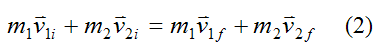
This equation can be expressed as its corresponding (scalar) equations along Cartesian x, y, z directions:




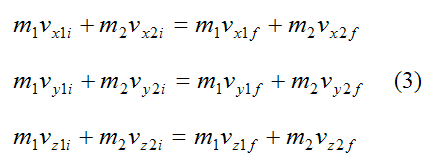
An additional equation needs to be introduced which accounts for the inelastic nature of the collision. Such an equation needs to relate the initial and final velocities of the particles. This is done using what is called the coefficient of restitution, e.

For instance, for the general case of collision between two particles the coefficient of restitution e can be used to relate the initial and final velocities along the line of impact, as shown below.



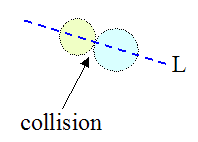
where L is the line of impact, passing through the centers of the particles.


The coefficient of restitution is given as



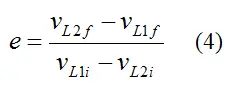
Where:

v_L1i is the component of the initial velocity of particle 1, resolved along the direction of L

v_L2i is the component of the initial velocity of particle 2, resolved along the direction of L

v_L1f is the component of the final velocity of particle 1, resolved along the direction of L

v_L2f is the component of the final velocity of particle 2, resolved along the direction of L


Equations (3) and (4) can be solved simultaneously.


For the special case of a head on inelastic collision in one dimension, the coefficient of restitution is



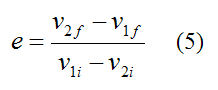
From equation (1) for the conservation of linear momentum, we have (in one dimension):




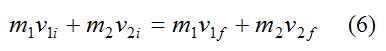
Equations (5) and (6) are then solved simultaneously.


The coefficient of restitution is determined experimentally for different classes of problems and types of materials. Its value varies between 0 and 1. For e = 1 the collision is elastic and kinetic energy is conserved. For e = 0 the collision is plastic, and the particles stick together and move with the same velocity, after impact.



Return to Dynamics page


Return to Real World Physics Problems home page