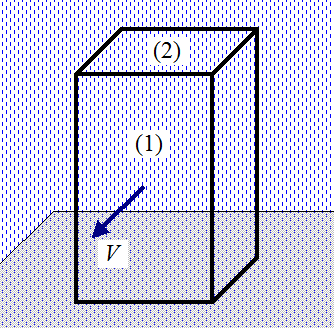
Mythbusters

The television show Mythbusters is one of the most popular science shows on television, and it uses a lot of physics!

I would often watch the show and eagerly look forward to the myths being tested. After I began watching it, it soon became obvious that the myths usually involve physics of some sort, especially classical mechanics in which there's motion and forces involved (such as when blowing things up). One can have a lot of fun trying to analyze the physics behind some of the myths that are tested. One of the myths that was tested on the show is: Is running better than walking to keep dry in the rain? It turns out you can analyze this myth in a fairly straightforward manner, and in this newsletter I will do just that.

First, model a person (moving through the rain) as an upright rectangular box moving through the rain at speed V as shown. The surface (1) represents the front of the person and the surface (2) represents the top of the person.

The figure below shows a side view of the set up.

Let w₁ be the rate of rain impingement on the front of the person (given as volume of water per second). Let w₂ be the rate of rain impingement on the top of the person (given as volume of water per second).

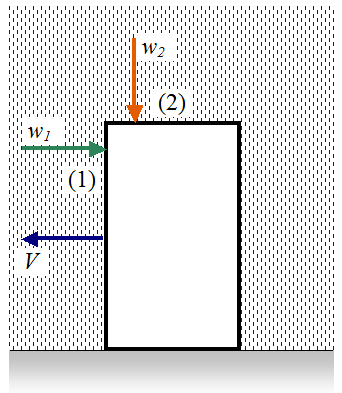
If the person is standing still w₁ = 0. If the person is moving then w₁ ≠ 0. The faster the person moves (at greater speed V) the greater is w₁.

The rate w₂ is always the same whether the person moves or not.

The rate w₁ is proportional to V. Mathematically this means that w₁ = aV, where a is a constant.

Let's say the person has to travel a distance d through the rain. We have to determine if this person should walk or run. The total amount (volume) of water that impinges on the front of the person as he/she travels the distance d is equal to A₁ = w₁T, where T is the total time (in seconds) it takes for the person to travel the distance d to their destination

Now, T = d/V, therefore A₁ = w₁(d/V) = aV(d/V) = ad, which is constant. Now, the total amount of water impinging on the person is A₁ + A₂, where A₂ is the amount (volume) of water impinging on the top of the person, and A₂ = w₂T. Since A₁ is constant, then to minimize getting wet we must minimize A₂. Since w₂ is always the same no matter what V is, then to minimize A₂ we must minimize the time T spent in the rain. Therefore to minimize getting wet the person must run as fast as he/she can to their destination. We are done!