About me and why I created this physics website.

Inertial Reference Frame

An inertial reference frame is important when analyzing the motion of objects. Whenever we apply the equations of motion, such as the force equations or moment equations, the acceleration must be measured relative to a Newtonian or inertial reference frame. This is a coordinate system that does not rotate, and is either fixed in three-dimensional space or moves in a straight line at constant velocity (with zero acceleration).

Since (when applying the equations of motion) acceleration must be measured relative to an inertial reference frame, it follows that angular velocity and angular acceleration (such as for a rigid body) must also be measured relative to this frame, since these quantities directly affect the acceleration.

Any forces that are acting on an object are a result of the acceleration of this object relative to an inertial reference frame. Thus, if we want to accurately predict the force F acting on an object, we must find its acceleration relative to an inertial reference frame and apply the equations of motion (e.g. F = ma) to find the force.

When applying the equations of motion for problems on earth, it is common practice to “attach” a coordinate system to the ground and assume that this is an inertial reference frame. However, it is not quite, since the earth itself rotates and the earth in turn revolves around the sun, etc. However, the rotation rate of a (ground) reference frame attached to the earth is very small, and its acceleration is also very small, so for practical purposes it can be treated as an inertial reference frame.

To show this, let’s determine the rotation rate and acceleration of a ground reference frame attached to the earth (so that it moves with the earth).

The rotation rate of the earth is one full revolution (2π rad) every 24 hours. The angular velocity (rotation rate) of the earth is therefore w = 7.3×10^-5 rad/s. This is equal to the rotation rate of the ground reference frame. As you can see, it is very small.

The acceleration of this reference frame is due to rotation of the earth, which causes centripetal acceleration. The maximum centripetal acceleration is at the equator, since the radius (perpendicular to the axis of earth’s rotation) is greatest there.

The radius of the earth at the equator is R = 6,400 km = 6,400,000 m.

The centripetal acceleration is w²R = 0.034 m/s². This is equal to the maximum possible acceleration of the ground reference frame. This is also very small. This becomes obvious if we compare it to the acceleration due to gravity, which on earth is 9.8 m/s².

There is also the affect of the rotation of the earth around the sun, and the rotation of our solar system within our galaxy. But these effects are also negligible.

Therefore, a ground reference frame attached to earth can be treated (with a high degree of accuracy) as an inertial reference frame.


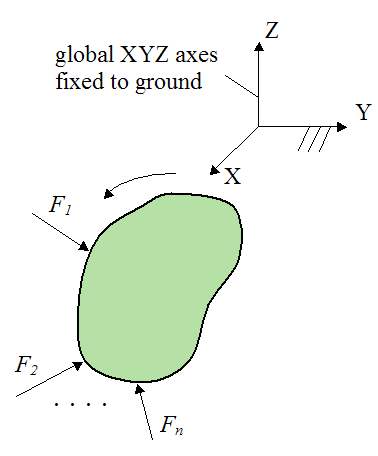
The figure below illustrates a typical set up of a dynamics problem that is solved using a global XYZ axis (fixed to ground). This is a coordinate system which serves as an inertial reference frame.

For example, we can accurately solve for the forces F₁, F₂,..., F_n acting on the body given its acceleration relative to the global XYZ axes.





Return to Dynamics page


Return to Real World Physics Problems home page