About me and why I created this physics website.

Gyro Top

The figure below shows a gyro top experiencing a state of general motion. The motion is such that the vectors w_n and α_n are always in the XY plane, and the vectors w_p and α_p are always in the Z-direction.




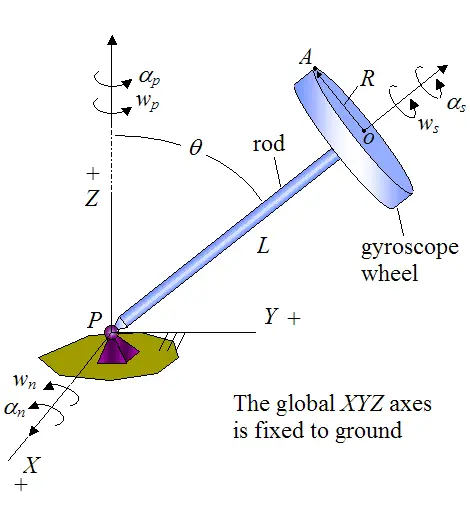
At the instant shown, determine the angular velocity and angular acceleration of the gyroscope wheel. Also, determine the velocity and acceleration of point A on the wheel.


Solution

We define the following:

At the instant shown, the unit vectors I, J, K are pointing along the positive X, Y, Z axis, respectively. In addition, these unit vectors are allowed to “move” with their corresponding angular velocity vectors (i.e. change orientation) as a way of accounting for the change in direction of each of the angular velocity vectors (w_s, w_p, w_n), as will be shown below.


Let's find the angular acceleration of the gyroscope wheel.

To do this, it is easiest to find the angular acceleration of each angular velocity vector (and then add them together). You do this by examining how each of the angular velocity vectors (w_s, w_p, w_n) moves, based on the kinematics of the problem.

First, calculate the angular acceleration of the angular velocity vector w_s. Call this vector w₁.



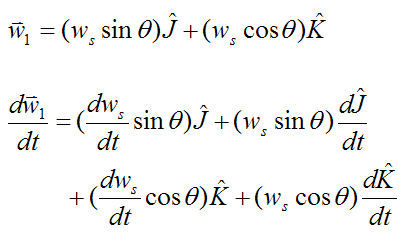
where




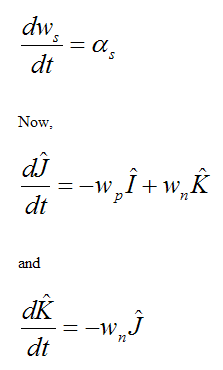
Second, calculate the angular acceleration of the angular velocity vector w_n. Call this vector w₂.




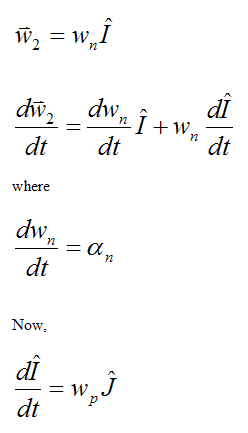
Third, calculate the angular acceleration of the angular velocity vector w_p. Call this vector w₃.



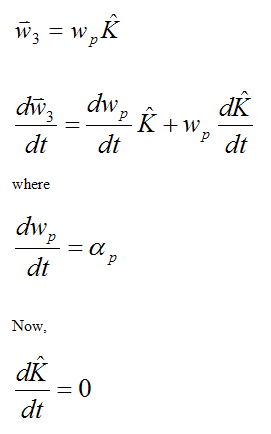
(there is no change in direction of the angular velocity vector w_p).


The angular velocity of the gyroscope wheel is:




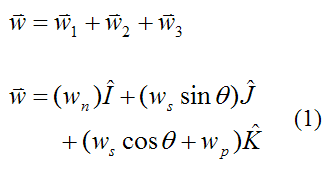
The angular acceleration of the gyroscope wheel is:




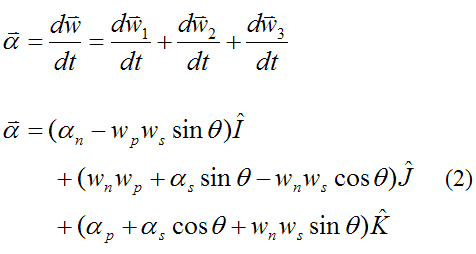
Note: The above expressions for dw₁/dt, dw₂/dt, and dw₃/dt are evaluated using vector derivatives.


Note that we are following the right-hand rule here. If any of the vectors w_s, w_p, w_n, α_s, α_p, α_n are spinning in the opposite direction to that shown in the diagram, you simply change the sign of those vectors to correct for that. For example, if w_n and α_s are acting in the opposite direction to that shown in the diagram, you replace w_n with (-w_n) and α_s with (-α_s), in equations (1) and (2).

There are some instances where the kinematics of the problem is unknown (not prescribed as it is here), so you cannot directly calculate the angular acceleration the way it is done here. Instead you have to treat it as an unknown in the problem. For an example of this, see the physics of bowling.



Let's now determine the velocity and acceleration of point A on the gyroscope wheel at the instant shown.

The general velocity equation for point A is



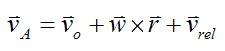
Where:

v_o is the velocity of point o on the gyro top rod (this point coincides with the center of the gyroscope wheel, on the front face)

w is the angular velocity of the gyroscope wheel, given by equation (1)

r is the position vector from point o to point A


Since point A is fixed on the wheel,




Let's first determine the velocity of point o on the gyro top rod (v_o), using the following general equation for velocity applied to point o:



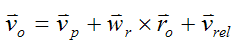
Where:

v_p is the velocity of point P on the rod

w_r is the angular velocity of the rod

r_o is the position vector from point P to point o


Since point o is fixed on the gyro top rod,



and



Therefore, we have




Due to the kinematics of the gyro top, the angular velocity of the rod is not affected by the angular velocity of the gyroscope wheel. Therefore, the angular velocity of the rod is determined by setting w_s = 0 in equation (1). This gives us



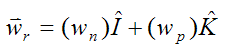
The position vector from point P to point o is



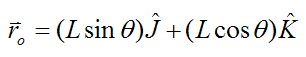
Substitute the above two equations into equation (3) to get the velocity v_o.


From before, the general velocity equation for calculating the velocity of point A is



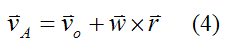
The position vector from point o to point A is



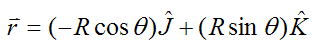
We can now calculate the velocity of point A using equation (4).



The general acceleration equation for point A is



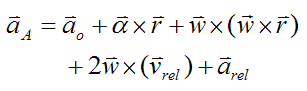
Where:

a_o is the acceleration of point o on the rod (this point coincides with the center of the gyroscope wheel, on the front face)

α is the angular acceleration of the gyroscope wheel, given by equation (2)

r is the position vector from point o to point A


Since point A is fixed on the wheel,




Let's first determine the acceleration of point o on the rod (a_o), using the following general equation for acceleration applied to point o:



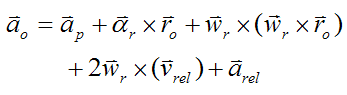
Where:

a_p is the acceleration of point P on the rod

α_r is the angular acceleration of the rod

r_o is the position vector from point P to point o

w_r is the angular velocity of the rod


Since point o is fixed on the rod,



and



Therefore, we have



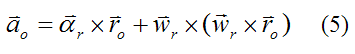
From before, the angular velocity of the rod is




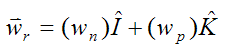
Due to the kinematics of the gyro top, the angular acceleration of the rod is not affected by the angular acceleration of the gyroscope wheel. Therefore, the angular acceleration of the rod is given by setting set w_s = 0 and α_s = 0 in equation (2). This gives us



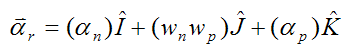
From before, the position vector from point P to point o is



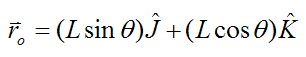
Substitute the above three equations into equation (5) to get the acceleration a_o.


From before, the general acceleration equation for calculating the acceleration of point A is



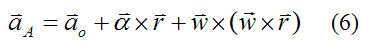
where w is given by equation (1), and α is given by equation (2).

From before, the position vector from point o to point A is



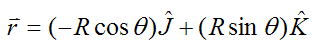
We can now calculate the acceleration of point A using equation (6).


Note that equations (3), (4), (5), (6) use vector cross product multiplication. To evaluate the vector cross product for two general vectors A and B (relative to the XYZ frame) use the following formula:





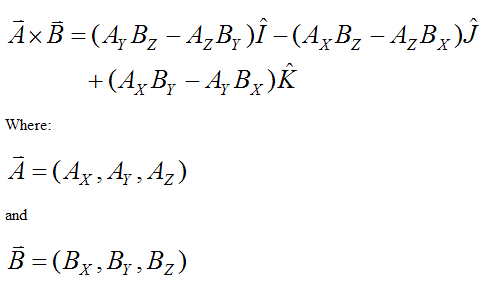
Return to Kinematics page


Return to Real World Physics Problems home page