About me and why I created this physics website.
Equilibrium
Equilibrium For A Particle
A particle is defined as being in equilibrium if it is stationary (at rest), or moving at constant velocity, with respect to ground (an inertial reference frame). This means that the vector sum of all the forces acting on it is equal to zero. See figure below.
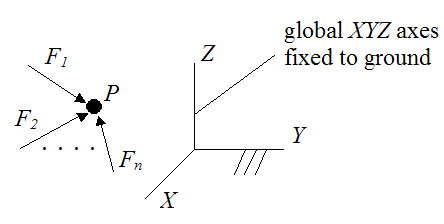
where F1, F2,..., Fn are the external forces acting on the particle P, and XYZ is an inertial reference frame fixed to ground.
By Newton’s Second Law,
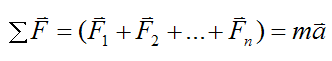
where ΣF is the vector sum of the forces, m is the mass of the particle, and a is the acceleration of the particle with respect to ground.
The particle P is in equilibrium if
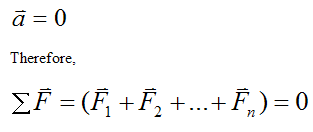
As a result, we can write the following scalar equations for the component directions of the sum of forces (along the X, Y, Z directions):
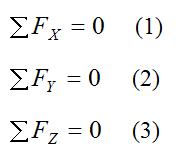
Where:
ΣFX is the sum of the forces in the X-direction
ΣFY is the sum of the forces in the Y-direction
ΣFZ is the sum of the forces in the Z-direction
More specifically,
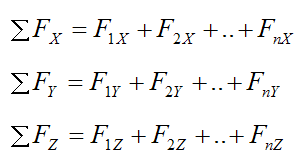
Where:
F1X, F2X,..., FnX are the X-components of the external forces acting on the particle P
F1Y, F2Y,..., FnY are the Y-components of the external forces acting on the particle P
F1Z, F2Z,..., FnZ are the Z-components of the external forces acting on the particle P
Equations (1)-(3) are all the equations that are necessary to solve for the forces on a particle in equilibrium.
Equilibrium For A Rigid Body
A rigid body is defined as being in equilibrium if:
• It is stationary (at rest), with respect to ground (an inertial reference frame).
• It is moving at constant velocity, with no rotation, with respect to ground.
These two conditions mean that the vector sum of all the forces acting on the rigid body is equal to zero. See figure below.
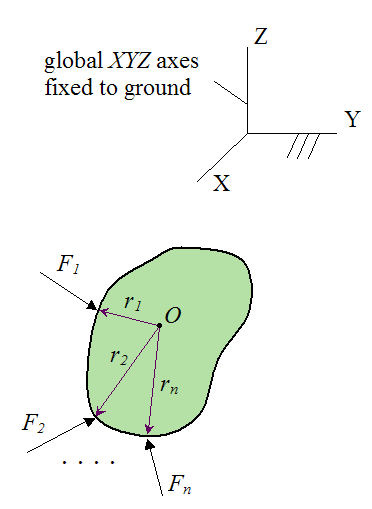
Where:
XYZ is an inertial reference frame fixed to ground
O is an arbitrary point, which can be located anywhere (on or off the rigid body)
F1, F2,..., Fn are the external forces acting on the rigid body
r1, r2,..., rn are the position vectors from point O to the locations on the rigid body where the external forces F1, F2,..., Fn are acting
By Newton’s Second Law,
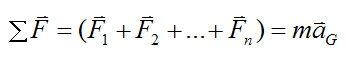
where ΣF is the vector sum of the forces, m is the mass of the rigid body, and aG is the acceleration of the center of mass G of the rigid body, with respect to ground.
The rigid body is in equilibrium if
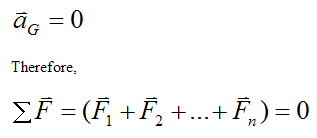
As a result, we can write the following scalar equations for the component directions of the sum of forces (along the X, Y, Z directions):
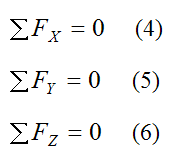
Where:
ΣFX is the sum of the forces in the X-direction
ΣFY is the sum of the forces in the Y-direction
ΣFZ is the sum of the forces in the Z-direction
More specifically,
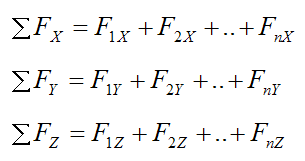
Where:
F1X, F2X,..., FnX are the X-components of the external forces acting on the rigid body
F1Y, F2Y,..., FnY are the Y-components of the external forces acting on the rigid body
F1Z, F2Z,..., FnZ are the Z-components of the external forces acting on the rigid body
The rigid body must also be in rotational equilibrium. This means that the sum of the moments about point O must equal zero. Thus, we can write the following scalar equations:
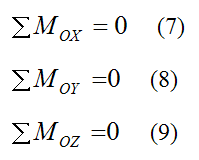
Where:
ΣMOX is the sum of the moments acting on the rigid body, taken about point O and about the X-direction
ΣMOY is the sum of the moments acting on the rigid body, taken about point O and about the Y-direction
ΣMOZ is the sum of the moments acting on the rigid body, taken about point O and about the Z-direction
Now,
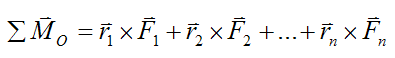
where ΣMO is the sum-of-moments vector
We can express ΣMO as its vector components:
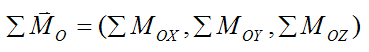
where ΣMOX, ΣMOY, ΣMOZ are the terms on the left side of the (scalar) equations (7)-(9).
Equations (4)-(9) are all the equations that are necessary to solve for the forces on a rigid body in equilibrium.
Once again, point O can be chosen arbitrarily. However, it is generally easiest to place O at a location where one of the external forces is acting (for example, F1), since this will result in the corresponding position vector (r1) equaling zero. This will eliminate the force F1 from the set of equations, thus reducing the number of unknowns to solve for in equations (4)-(9).
For planar problems (two-dimensional) you can place O at the intersection of the lines of action of any two unknown external forces. This will eliminate those two forces from the equations, since the moment of those forces will be zero (i.e. r×F = 0, since the position vector r and the force vector F are parallel, for these two forces).
For more information on moments see moment of a force.
For example problems involving equilibrium see:
Physics Of Skydiving
Wheel rolling at constant speed
If you want to test your understanding and solve some problems go to Statics Problems.
Return to Dynamics page
Return to Real World Physics Problems home page