About me and why I created this physics website.

Circular Motion Problems

On this page I put together a collection of circular motion problems to help you understand circular motion better. The required equations and background reading to solve these problems is given on the rotational motion page.

Refer to the figure below for problems 1-6.

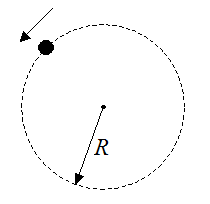
circular motion problems figure 1


Problem # 1

A particle is traveling in a circle of radius R = 1.5 m and with an angular velocity of 10 rad/s. What is the tangential velocity of the particle? (Answer: 15 m/s)


Problem # 2

A particle is traveling in a circle of radius R = 2.5 m and with an angular velocity of 10 rad/s. What is the centripetal acceleration of the particle? (Answer: 250 m/s2)


Problem # 3

The particle in problem # 2 begins to slow down with an angular acceleration of -1 rad/s2. After 5 seconds, what is the centripetal acceleration and the tangential acceleration of the particle? (Answer: 62.5 m/s2, -2.5 m/s2)


Problem # 4

What is the magnitude of the total acceleration of the particle in problem # 3, after 5 seconds? (Answer: 62.55 m/s2)


Problem # 5

A particle is moving around in a circle of radius R = 1.5 m with a constant speed of 2 m/s. What is the centripetal acceleration and angular velocity of the particle? (Answer: 2.67 m/s2, 1.33 rad/s)


Problem # 6

The particle in problem # 5 begins to accelerate tangentially at 3 m/s2. What is the speed of the particle at this instant and what is the magnitude of the total acceleration of the particle at this instant? (Answer: 2 m/s, 4.014 m/s2)


Problem # 7

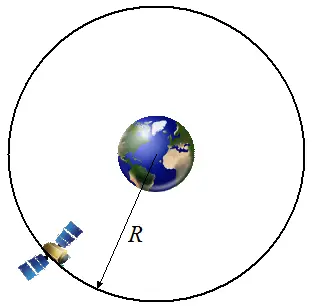
circular motion problems figure 2

A geostationary orbit is a circular orbit above the earth's equator. An object in such an orbit has an orbital period equal to the earth's rotational period, and therefore appears motionless in the sky relative to ground observers. This is useful for communication and weather satellites since antennas on earth do not have to track them and instead are pointed in a permanent direction at the orbiting satellites.

Using Newton's Law of Gravitational Attraction, a mass of earth equal to 5.9736 × 1024 kg, and an orbital period of 23 hours, 56 minutes, 4.0916 seconds, calculate the radius R of a geostationary orbit around the earth. (Answer: 42164 km)



Bonus Problems Related to Circular Motion

1. Can a standard CD-ROM drive shatter a CD when spinning at high speed?

2. When a bus is going around a turn at over 50 miles per hour, will moving passengers to the inside of the turn keep the bus from flipping?

I created a physics analysis for these two problems, in PDF format. It's available through this link.



Return to Kinematics page


Return to Real World Physics Problems home page